COSMOS v7.655  COSMOSv7655
(AirShowerMC)
Functions/Subroutines
genas.f File Reference

Go to the source code of this file.

Functions/Subroutines

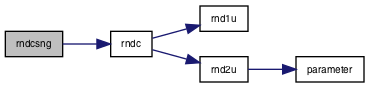
subroutine rndcsng (u)
 
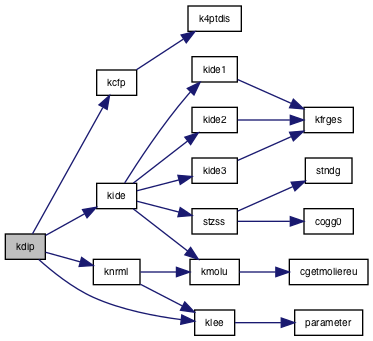
subroutine kdigb0 (e0, cosz, s, r, rho)
 
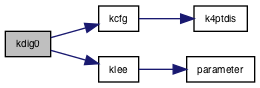
subroutine kdig0 (e0, cosz, s, r, rho)
 
subroutine kdipb0 (e0, cosz, s, r, rho)
 
subroutine kdip0 (e0, cosz, s, r, rho)
 
subroutine kudig (e0, zob, cosz, s, de, j1, r, rho)
 
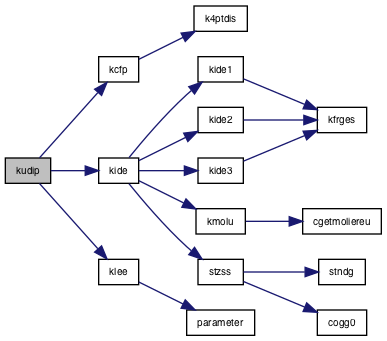
subroutine kudip (e0, zob, cosz, s, de, j1, r, rho)
 
subroutine kudigb (e0, zob, cosz, s, de, j1, r, rho)
 
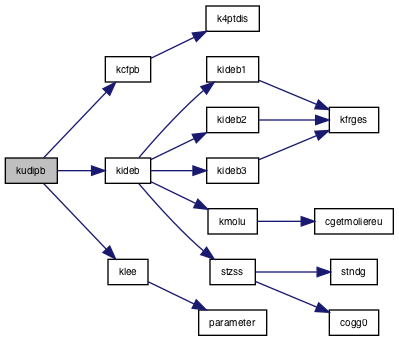
subroutine kudipb (e0, zob, cosz, s, de, j1, r, rho)
 
subroutine kcfg (e0, cosz, s, r, cf)
 
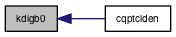
subroutine kcfgb (e0, cosz, s, r, cf)
 
subroutine kcfp (e0, cosz, s, r, cf)
 
subroutine kcfpb (e0, cosz, s, r, cf)
 
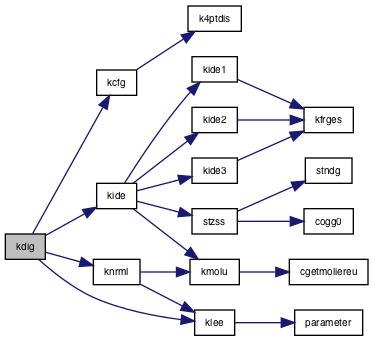
subroutine kdig (e0, zob, cosz, s, de, j1, r, rho)
 
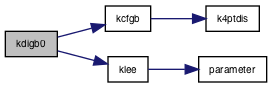
subroutine kdip (e0, zob, cosz, s, de, j1, r, rho)
 
subroutine kdigb (e0, zob, cosz, s, de, j1, r, rho)
 
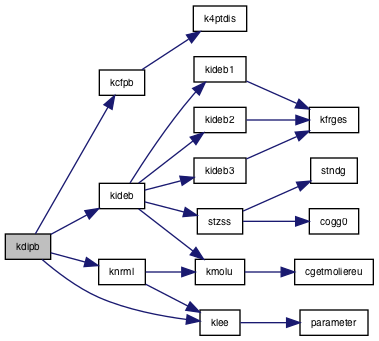
subroutine kdipb (e0, zob, cosz, s, de, j1, r, rho)
 
subroutine kefg (cosz, s, ef)
 
subroutine kefp (cosz, s, ef)
 
subroutine kefgb (cosz, s, ef)
 
subroutine kefpb (cosz, s, ef)
 
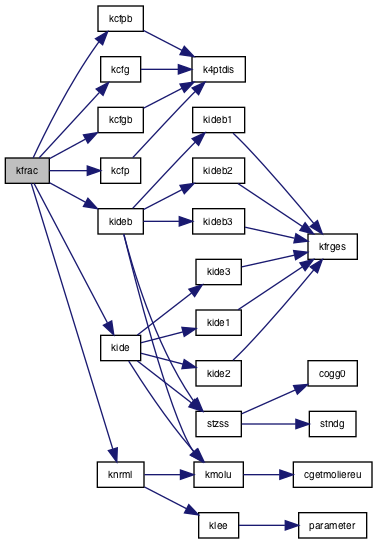
subroutine kfrac (jsc, k, e0, zob, cosz, s, pmin, frac)
 
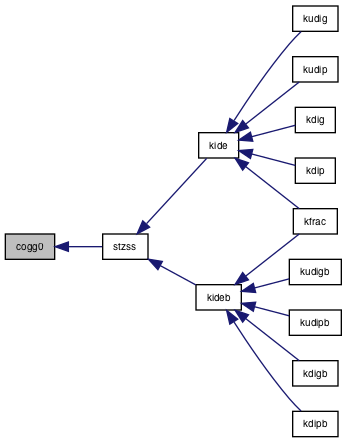
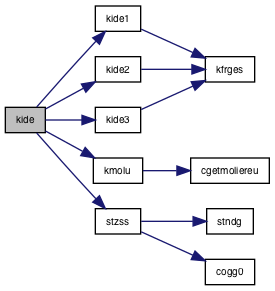
subroutine kide (e0, zob, s, cosz, j1, rr, de, fr)
 
subroutine kideb (e0, zob, s, cosz, j1, rr, de, fr)
 
subroutine kideb1 (de, r, fr)
 
subroutine kideb2 (de, r, fr)
 
subroutine kideb3 (de, r, fr)
 
subroutine kide1 (de, r, fr)
 
subroutine kide2 (de, r, fr)
 
subroutine kide3 (de, r, fr)
 
subroutine kintp3s (f, intv, n, x1, h, x, ans)
 
subroutine kfrges (x, intvx, n, c, m, icon)
 
subroutine kgausss (av, s, x1, x2)
 
subroutine k4ptdis (f, im, jm, iadj, x0, y0, hx, hy, x, y, ans)
 
subroutine klee (s, r, rho)
 

kklibg >>>>>>>>>>>>>>>>>>>>>>>>>>>>

More...
 
subroutine kmolu (dep, cosz, rmu)
 
subroutine knrml (e0, zob, cosz, s, de, kcfx, kidx, sum)
 
subroutine knrml2 (e0, zob, cosz, s, discle, kcfx, kidx, sum)
 
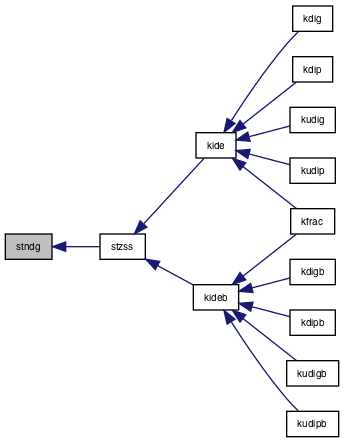
subroutine stzss (S, Z)
 
subroutine stndg (ELG, S, Z)
 
subroutine cogg0 (EL, COG)
 

Function/Subroutine Documentation

◆ cogg0()

subroutine cogg0 (   EL,
  COG 
)

Definition at line 3771 of file genas.f.

Referenced by stzss().

3771  cog=85.4*el + 347.5
Here is the caller graph for this function:

◆ k4ptdis()

subroutine k4ptdis ( dimension(iadj,jm)  f,
  im,
  jm,
  iadj,
  x0,
  y0,
  hx,
  hy,
  x,
  y,
  ans 
)

Definition at line 3533 of file genas.f.

References a, b, f, i, j, p, x, and y.

Referenced by kcfg(), kcfgb(), kcfp(), and kcfpb().

3533  dimension f(iadj,jm)
3534 !
3535  a=(x-x0)/hx
3536  b=(y-y0)/hy
3537  i=a
3538  j=b
3539  i=min0(max0(i,0)+1,im-1)
3540  j=min0(max0(j,0)+1,jm-1)
3541  p=a+1.-i
3542  q=b+1.-j
3543  p1=1.-p
3544  q1=1.-q
3545  ans=( f(i,j)*p1 + f(i+1,j)*p ) * q1 +
3546  * ( f(i,j+1)*p1 + f(i+1,j+1)*p ) * q
3547  return
ans
atmos%rho(atmos%nodes) **exp(-(z-atmos%z(atmos%nodes))/Hinf) elseif(z .lt. atmos%z(1)) then ans=atmos%rho(1) **exp((atmos%z(1) -z)/atmos%H(1)) else call kdwhereis(z, atmos%nodes, atmos%z, 1, i) a=atmos%a(i) if(a .ne. 0.d0) then ans=atmos%rho(i) **(1+a *(z-atmos%z(i))/atmos%H(i)) **(-1.0d0-1.d0/a) else ans=*atmos%rho(i) *exp(-(z-atmos%z(i))/atmos%H(i)) endif endif ! zsave=z ! endif cvh2den=ans end ! ---------------------------------- real *8 function cvh2temp(z) implicit none ! vettical height to temperatur(Kelvin) real *8 z ! input. vertical height in m ! output is temperature of the atmospher in Kelvin real *8 ans integer i if(z .gt. atmos%z(atmos%nodes)) then ans=atmos%T(atmos%nodes) elseif(z .lt. atmos%z(1)) then ans=atmos%T(1)+atmos%b(1) *(z - atmos%z(1)) else call kdwhereis(z, atmos%nodes, atmos%z, 1, i) ans=atmos%T(i)+atmos%b(i) *(z-atmos%z(i)) endif cvh2temp=ans end !--------------------------------------------- real *8 function cthick2h(t) implicit none real *8 t ! input. air thickness in kg/m^2 real *8 logt, ans integer i real *8 dod0, fd, a logt=log(t) if(t .ge. atmos%cumd(1)) then ans=atmos%z(1) - *(logt - atmos%logcumd(1)) *atmos%H(1) elseif(t .le. atmos%cumd(atmos%nodes)) then ans=atmos%z(atmos%nodes) - *Hinf *log(t/atmos%cumd(atmos%nodes)) else call kdwhereis(t, atmos%nodes, atmos%cumd, 1, i) ! i is such that X(i) > x >=x(i+1) ans
Definition: cstdatmos0.fNew2.h:82
i
nodes i
Definition: cstdatmos0.fNew2.h:93
p
********************block data cblkHeavy ********************integer j data *HeavyG2symbol p
Definition: cblkHeavy.h:7
j
********************block data cblkHeavy ********************integer j data *HeavyG2symbol *data *HeavyG2code kiron data j
Definition: cblkHeavy.h:36
y
latitude latitude this system is used *****************************************************************! type coord sequence union map real y
Definition: Zcoord.h:25
nrl_atmos::a
real(4), save a
Definition: cNRLAtmos.f:20
nrl_atmos::b
real(4), save b
Definition: cNRLAtmos.f:21
x
! structure defining a particle at production ! Basic idea of what is to be contained in ! the particle structue is that dynamical ones should be included those derivable from the particle code ! is not included ******************************************************type fmom momentum sequence union map real e endmap map real * x
Definition: Zptcl.h:21
f
dE dx *! Nuc Int sampling table f
Definition: cblkMuInt.h:130
Here is the caller graph for this function:

◆ kcfg()

subroutine kcfg (   e0,
  cosz,
  s,
  r,
  cf 
)

Definition at line 1765 of file genas.f.

References e, i, k4ptdis(), and r.

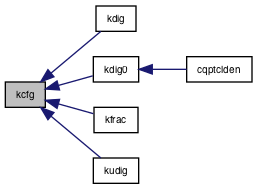
Referenced by kdig(), kdig0(), kfrac(), and kudig().

1765 ! e0: input. 1ry energy in tev.
1766 ! at present not used.
1767 ! cosz: input. cos of zenith
1768 ! s: input. age of the gamma shower
1769 ! for s<.4 or >1.6 not accurate.
1770 ! r: input. distance measured in moliere unit.
1771 ! moliere unit should be at 2r.l above the observation
1772 ! depth (along 1ry direction).
1773 ! cf: output. correction factor.
1774 ! cf*rho(s,r) gives normalized lateral distribution
1775 ! for particles giving de>0 in scinti.
1776 ! rho is the output from klee.
1777  dimension rat(35, 11)
1778  dimension dty1(35), dty2(35), dty3(35), dty4(35), dty5(35)
1779  dimension dty6(35), dty7(35), dty8(35), dty9(35), dty10(35)
1780  dimension dty11(35)
1781  equivalence(rat(1,1), dty1(1))
1782  equivalence(rat(1,2), dty2(1))
1783  equivalence(rat(1,3), dty3(1))
1784  equivalence(rat(1,4), dty4(1))
1785  equivalence(rat(1,5), dty5(1))
1786  equivalence(rat(1,6), dty6(1))
1787  equivalence(rat(1,7), dty7(1))
1788  equivalence(rat(1,8), dty8(1))
1789  equivalence(rat(1,9), dty9(1))
1790  equivalence(rat(1,10), dty10(1))
1791  equivalence(rat(1,11), dty11(1))
1792 ! gamma fe.1sc3.5/lee s=.5
1793 ! rho*/rho=cf: log10(cf) for log10(r)=-3.815 to 1.6 step .160
1794 ! s=0.5
1795  data (dty1(i),i= 1, 35)/
1796  1 -0.114, -0.052, -0.003, 0.015, 0.040, 0.053, 0.060, 0.061,
1797  2 0.056, 0.056, 0.045, 0.028, -0.001, -0.043, -0.066, -0.077,
1798  3 -0.076, -0.076, -0.081, -0.074, -0.055, -0.024, 0.031, 0.092,
1799  4 0.183, 0.304, 0.461, 0.667, 0.818, 0.928, 0.995, 1.050,
1800  5 1.081, 1.088, 1.082/
1801 ! s=0.6
1802  data (dty2(i),i= 1, 35)/
1803  1 -0.138, -0.095, -0.070, -0.045, -0.014, -0.007, 0.000, -0.012,
1804  2 -0.011, -0.010, -0.015, -0.008, -0.026, -0.043, -0.066, -0.077,
1805  3 -0.083, -0.082, -0.087, -0.080, -0.067, -0.048, -0.018, 0.037,
1806  4 0.110, 0.178, 0.275, 0.420, 0.566, 0.729, 0.862, 0.923,
1807  5 0.942, 0.943, 0.908/
1808 ! s=0.7
1809  data (dty3(i),i= 1, 35)/
1810  1 -0.240, -0.179, -0.136, -0.105, -0.080, -0.055, -0.048, -0.048,
1811  2 -0.041, -0.040, -0.039, -0.038, -0.050, -0.055, -0.060, -0.071,
1812  3 -0.089, -0.100, -0.093, -0.086, -0.067, -0.055, -0.011, 0.049,
1813  4 0.123, 0.196, 0.299, 0.414, 0.559, 0.675, 0.742, 0.767,
1814  5 0.737, 0.672, 0.588/
1815 ! s=0.8
1816  data (dty4(i),i= 1, 35)/
1817  1 -0.336, -0.257, -0.202, -0.159, -0.122, -0.091, -0.079, -0.066,
1818  2 -0.047, -0.046, -0.039, -0.044, -0.050, -0.061, -0.060, -0.071,
1819  3 -0.089, -0.076, -0.093, -0.092, -0.073, -0.048, -0.023, 0.037,
1820  4 0.105, 0.184, 0.287, 0.402, 0.517, 0.608, 0.658, 0.628,
1821  5 0.563, 0.449, 0.347/
1822 ! s=0.9
1823  data (dty5(i),i= 1, 35)/
1824  1 -0.421, -0.330, -0.269, -0.214, -0.158, -0.121, -0.097, -0.072,
1825  2 -0.065, -0.058, -0.051, -0.056, -0.062, -0.079, -0.084, -0.089,
1826  3 -0.101, -0.082, -0.087, -0.086, -0.079, -0.054, -0.024, 0.019,
1827  4 0.074, 0.153, 0.245, 0.348, 0.469, 0.524, 0.489, 0.393,
1828  5 0.298, 0.208, 0.125/
1829 ! sw=1.0
1830  data (dty6(i),i= 1, 34)/
1831  1 -0.487, -0.402, -0.323, -0.262, -0.201, -0.164, -0.127, -0.108,
1832  2 -0.089, -0.070, -0.069, -0.063, -0.068, -0.067, -0.078, -0.089,
1833  3 -0.107, -0.105, -0.104, -0.085, -0.061, -0.036, 0.001, 0.056,
1834  4 0.117, 0.203, 0.312, 0.397, 0.464, 0.435, 0.351, 0.268,
1835  5 0.184, 0.125/
1836 ! s=1.1
1837  data (dty7(i),i= 1, 35)/
1838  1 -0.638, -0.540, -0.449, -0.364, -0.297, -0.236, -0.181, -0.138,
1839  2 -0.113, -0.094, -0.069, -0.069, -0.062, -0.055, -0.066, -0.095,
1840  3 -0.101, -0.100, -0.093, -0.080, -0.079, -0.061, -0.030, 0.001,
1841  4 0.050, 0.123, 0.184, 0.282, 0.367, 0.428, 0.392, 0.297,
1842  5 0.219, 0.154, 0.106/
1843 ! s=1.2
1844  data (dty8(i),i= 1, 35)/
1845  1 -0.740, -0.631, -0.516, -0.424, -0.339, -0.266, -0.211, -0.162,
1846  2 -0.125, -0.094, -0.075, -0.062, -0.068, -0.073, -0.078, -0.089,
1847  3 -0.101, -0.112, -0.111, -0.098, -0.085, -0.061, -0.030, 0.007,
1848  4 0.050, 0.117, 0.178, 0.240, 0.337, 0.380, 0.362, 0.297,
1849  5 0.219, 0.154, 0.076/
1850 ! s=1.3
1851  data (dty9(i),i= 1, 35)/
1852  1 -0.836, -0.685, -0.564, -0.460, -0.369, -0.302, -0.253, -0.192,
1853  2 -0.155, -0.118, -0.093, -0.069, -0.074, -0.067, -0.078, -0.095,
1854  3 -0.113, -0.118, -0.117, -0.122, -0.110, -0.091, -0.066, -0.035,
1855  4 0.002, 0.069, 0.142, 0.209, 0.294, 0.350, 0.326, 0.285,
1856  5 0.219, 0.148, 0.088/
1857 ! s=1.4
1858  data (dty10(i),i= 1, 35)/
1859  1 -0.897, -0.763, -0.624, -0.466, -0.339, -0.260, -0.205, -0.144,
1860  2 -0.107, -0.064, -0.057, -0.044, -0.062, -0.061, -0.072, -0.095,
1861  3 -0.113, -0.142, -0.153, -0.146, -0.134, -0.109, -0.084, -0.047,
1862  4 -0.004, 0.051, 0.130, 0.209, 0.252, 0.313, 0.320, 0.267,
1863  5 0.189, 0.100, 0.052/
1864 ! s=1.5
1865  data (dty11(i),i= 1, 35)/
1866  1 -0.993, -0.878, -0.732, -0.581, -0.442, -0.314, -0.211, -0.138,
1867  2 -0.083, -0.058, -0.063, -0.062, -0.062, -0.073, -0.084, -0.107,
1868  3 -0.125, -0.148, -0.165, -0.171, -0.164, -0.163, -0.138, -0.101,
1869  4 -0.052, 0.009, 0.094, 0.185, 0.258, 0.301, 0.290, 0.243,
1870  5 0.165, 0.088, 0.046/
1871 !
1872 ! effective s
1873 !cc rs=1. - 1./(1. + exp(r-8.))
1874 !cc si=s*( -0.0285 *log10(e0/100.)*rs + 1.)
1875  si = s ! not use above
1876 
1877  if(si .lt. .4) then
1878  si=.4
1879  elseif(si .gt. 1.6) then
1880  si=1.6
1881  endif
1882  if(r .lt. 1.e-4) then
1883  ri=1.e-4
1884  elseif(r .gt. 70.) then
1885  ri=70.
1886  else
1887  ri=r
1888  endif
1889 !c if(ri .gt. 8.) then
1890 !c c = -3.5*(cosz-1.) + 1.
1891 !c ri=(ri-8.)*c + 8.
1892 !c endif
1893  ri=log10(ri)
1894 !
1895  call
1896  * k4ptdis(rat, 35, 11, 35, -3.82, 0.5, .16, .1, ri, si, ans)
1897  cf=10.**(ans)
e
dE dx *! Nuc Int sampling table e
Definition: cblkMuInt.h:130
ans
atmos%rho(atmos%nodes) **exp(-(z-atmos%z(atmos%nodes))/Hinf) elseif(z .lt. atmos%z(1)) then ans=atmos%rho(1) **exp((atmos%z(1) -z)/atmos%H(1)) else call kdwhereis(z, atmos%nodes, atmos%z, 1, i) a=atmos%a(i) if(a .ne. 0.d0) then ans=atmos%rho(i) **(1+a *(z-atmos%z(i))/atmos%H(i)) **(-1.0d0-1.d0/a) else ans=*atmos%rho(i) *exp(-(z-atmos%z(i))/atmos%H(i)) endif endif ! zsave=z ! endif cvh2den=ans end ! ---------------------------------- real *8 function cvh2temp(z) implicit none ! vettical height to temperatur(Kelvin) real *8 z ! input. vertical height in m ! output is temperature of the atmospher in Kelvin real *8 ans integer i if(z .gt. atmos%z(atmos%nodes)) then ans=atmos%T(atmos%nodes) elseif(z .lt. atmos%z(1)) then ans=atmos%T(1)+atmos%b(1) *(z - atmos%z(1)) else call kdwhereis(z, atmos%nodes, atmos%z, 1, i) ans=atmos%T(i)+atmos%b(i) *(z-atmos%z(i)) endif cvh2temp=ans end !--------------------------------------------- real *8 function cthick2h(t) implicit none real *8 t ! input. air thickness in kg/m^2 real *8 logt, ans integer i real *8 dod0, fd, a logt=log(t) if(t .ge. atmos%cumd(1)) then ans=atmos%z(1) - *(logt - atmos%logcumd(1)) *atmos%H(1) elseif(t .le. atmos%cumd(atmos%nodes)) then ans=atmos%z(atmos%nodes) - *Hinf *log(t/atmos%cumd(atmos%nodes)) else call kdwhereis(t, atmos%nodes, atmos%cumd, 1, i) ! i is such that X(i) > x >=x(i+1) ans
Definition: cstdatmos0.fNew2.h:82
r
*Zfirst p fm *Zfirst p Zfirst p Zfirst p *Zfirst p *Zfirst pos xyz r
Definition: ZavoidUnionMap.h:1
i
nodes i
Definition: cstdatmos0.fNew2.h:93
k4ptdis
subroutine k4ptdis(f, im, jm, iadj, x0, y0, hx, hy, x, y, ans)
Definition: genas.f:3533
Here is the call graph for this function:
Here is the caller graph for this function:

◆ kcfgb()

subroutine kcfgb (   e0,
  cosz,
  s,
  r,
  cf 
)

Definition at line 1927 of file genas.f.

References e, i, k4ptdis(), and r.

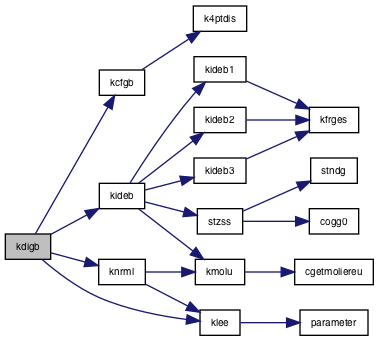
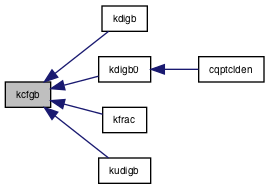
Referenced by kdigb(), kdigb0(), kfrac(), and kudigb().

1927 ! e0: input. 1ry energy in tev.
1928 ! at present not used.
1929 ! cosz: input. cos of zenith
1930 ! s: input. age of the gamma shower
1931 ! for s<.4 or >1.7 not accurate.
1932 ! r: input. distance measured in moliere unit.
1933 ! moliere unit should be at 2r.l above the observation
1934 ! depth (along 1ry direction).
1935 ! cf: output. correction factor.
1936 ! cf*rho(s,r) gives normalized lateral distribution
1937 ! for particles giving de>0 in scinti.
1938 ! rho is the output from klee.
1939  dimension rat(35, 14)
1940  dimension dty1(35), dty2(35), dty3(35), dty4(35), dty5(35)
1941  dimension dty6(35), dty7(35), dty8(35), dty9(35), dty10(35)
1942  dimension dty11(35), dty12(35), dty13(35), dty14(35)
1943  equivalence(rat(1,1), dty1(1))
1944  equivalence(rat(1,2), dty2(1))
1945  equivalence(rat(1,3), dty3(1))
1946  equivalence(rat(1,4), dty4(1))
1947  equivalence(rat(1,5), dty5(1))
1948  equivalence(rat(1,6), dty6(1))
1949  equivalence(rat(1,7), dty7(1))
1950  equivalence(rat(1,8), dty8(1))
1951  equivalence(rat(1,9), dty9(1))
1952  equivalence(rat(1,10), dty10(1))
1953  equivalence(rat(1,11), dty11(1))
1954  equivalence(rat(1,12), dty12(1))
1955  equivalence(rat(1,13), dty13(1))
1956  equivalence(rat(1,14), dty14(1))
1957 ! rho(pb.5fe.1sc3.5)/lee for 10**14 e-; s=0.4
1958  data (dty1(i),i= 1, 35)/
1959  1 0.148, 0.155, 0.162, 0.151, 0.146, 0.129, 0.106, 0.089,
1960  2 0.060, 0.013, -0.028, -0.087, -0.140, -0.176, -0.199, -0.210,
1961  3 -0.209, -0.202, -0.195, -0.188, -0.169, -0.156, -0.125, -0.082,
1962  4 -0.033, 0.010, 0.047, 0.072, 0.097, 0.110, 0.087, 0.052,
1963  5 -0.013, -0.126, -0.264/
1964 ! s=.5
1965  data (dty2(i),i= 1, 35)/
1966  1 0.115, 0.128, 0.141, 0.154, 0.149, 0.144, 0.150, 0.121,
1967  2 0.110, 0.068, 0.033, -0.020, -0.068, -0.115, -0.144, -0.162,
1968  3 -0.173, -0.184, -0.195, -0.177, -0.170, -0.115, -0.078, -0.041,
1969  4 0.002, 0.051, 0.094, 0.143, 0.174, 0.199, 0.206, 0.140,
1970  5 0.057, -0.027, -0.267/
1971 ! s=0.6
1972  data (dty3(i),i= 1, 35)/
1973  1 0.063, 0.079, 0.103, 0.112, 0.113, 0.114, 0.100, 0.101,
1974  2 0.071, 0.034, 0.004, -0.026, -0.056, -0.085, -0.107, -0.122,
1975  3 -0.167, -0.181, -0.203, -0.195, -0.178, -0.146, -0.099, -0.006,
1976  4 0.087, 0.196, 0.305, 0.406, 0.491, 0.546, 0.547, 0.479,
1977  5 0.326, 0.020, -0.279/
1978 ! s=0.7
1979  data (dty4(i),i= 1, 35)/
1980  1 -0.002, 0.017, 0.036, 0.043, 0.043, 0.044, 0.033, 0.022,
1981  2 0.016, 0.005, -0.012, -0.035, -0.065, -0.088, -0.124, -0.153,
1982  3 -0.170, -0.176, -0.175, -0.168, -0.161, -0.100, -0.033, 0.041,
1983  4 0.144, 0.229, 0.339, 0.467, 0.564, 0.650, 0.693, 0.651,
1984  5 0.531, 0.145, -0.265/
1985 ! s=0.8
1986  data (dty5(i),i= 1, 35)/
1987  1 -0.047, -0.035, -0.022, -0.009, -0.009, -0.008, -0.013, -0.007,
1988 ! 2 -0.018, -0.017, -0.029, -0.034, -0.058, -0.075, -0.081, -0.086,
1989  2 -0.018, -0.017, -0.029, -0.046, -0.070, -0.086, -0.113, -0.130,
1990 ! 3 -0.097, -0.091, -0.090, -0.083, -0.071, -0.022, 0.045, 0.124,
1991  3 -0.155, -0.155, -0.149, -0.142, -0.108, -0.070, -0.005, 0.084,
1992  4 0.203, 0.306, 0.415, 0.554, 0.633, 0.700, 0.731, 0.719,
1993  5 0.636, 0.395, -0.158/
1994 ! s=0.9
1995  data (dty6(i),i= 1, 35)/
1996  1 -0.037, -0.021, 0.003, 0.012, 0.013, 0.022, 0.030, 0.031,
1997  2 0.033, -0.028, -0.019, -0.026, -0.033, -0.039, -0.069, -0.091,
1998  3 -0.113, -0.135, -0.150, -0.141, -0.155, -0.139, -0.084, -0.014,
1999  4 0.064, 0.158, 0.259, 0.367, 0.468, 0.523, 0.532, 0.448,
2000  5 0.296, 0.027, -0.325/
2001 ! s=1.0
2002  data (dty7(i),i= 1, 35)/
2003  1 -0.023, -0.004, 0.015, 0.021, 0.034, 0.035, 0.036, 0.042,
2004  2 0.043, 0.044, 0.039, 0.028, 0.016, -0.007, -0.042, -0.077,
2005  3 -0.100, -0.123, -0.128, -0.134, -0.115, -0.102, -0.071, 0.001,
2006  4 0.074, 0.171, 0.255, 0.352, 0.436, 0.467, 0.486, 0.421,
2007  5 0.308, 0.015, -0.295/
2008 ! s=1.1
2009  data (dty8(i),i= 1, 35)/
2010  1 0.017, 0.027, 0.036, 0.045, 0.047, 0.057, 0.058, 0.067,
2011  2 0.069, 0.063, 0.065, 0.051, 0.037, 0.008, -0.029, -0.058,
2012  3 -0.087, -0.093, -0.099, -0.105, -0.119, -0.102, -0.085, -0.037,
2013  4 0.034, 0.120, 0.229, 0.323, 0.409, 0.457, 0.466, 0.422,
2014  5 0.324, 0.094, -0.296/
2015 ! s=1.2
2016  data (dty9(i),i= 1, 35)/
2017  1 0.110, 0.135, 0.144, 0.145, 0.147, 0.149, 0.143, 0.136,
2018  2 0.123, 0.101, 0.088, 0.066, 0.045, 0.008, -0.021, -0.050,
2019  3 -0.087, -0.101, -0.115, -0.121, -0.119, -0.117, -0.093, -0.037,
2020  4 0.026, 0.112, 0.214, 0.308, 0.386, 0.419, 0.405, 0.368,
2021  5 0.254, 0.064, -0.312/
2022 ! s=1.3
2023  data (dty10(i),i= 1, 35)/
2024  1 0.240, 0.250, 0.244, 0.245, 0.232, 0.233, 0.235, 0.221,
2025  2 0.200, 0.178, 0.157, 0.120, 0.091, 0.046, 0.002, -0.035,
2026  3 -0.072, -0.093, -0.115, -0.121, -0.127, -0.118, -0.101, -0.053,
2027  4 0.018, 0.081, 0.175, 0.262, 0.340, 0.388, 0.397, 0.353,
2028  5 0.239, 0.041, -0.258/
2029 ! s=1.4
2030  data (dty11(i),i= 1, 35)/
2031  1 0.140, 0.181, 0.190, 0.215, 0.224, 0.218, 0.220, 0.213,
2032  2 0.200, 0.171, 0.134, 0.097, 0.045, 0.008, -0.029, -0.066,
2033  3 -0.087, -0.109, -0.115, -0.128, -0.127, -0.117, -0.093, -0.045,
2034  4 -0.036, 0.051, 0.129, 0.215, 0.302, 0.334, 0.343, 0.291,
2035  5 0.216, -0.013, -0.319/
2036 ! s=1.5
2037  data (dty12(i),i= 1, 35)/
2038  1 0.171, 0.196, 0.198, 0.215, 0.216, 0.210, 0.204, 0.198,
2039  2 0.169, 0.148, 0.118, 0.082, 0.045, 0.008, -0.021, -0.050,
2040  3 -0.095, -0.108, -0.130, -0.144, -0.150, -0.133, -0.124, -0.091,
2041  4 -0.043, 0.035, 0.083, 0.169, 0.248, 0.288, 0.289, 0.245,
2042  5 0.170, 0.018, -0.311/
2043 ! s=1.6
2044  data (dty13(i),i= 1, 35)/
2045  1 0.117, 0.150, 0.159, 0.161, 0.170, 0.164, 0.158, 0.152,
2046  2 0.131, 0.101, 0.072, 0.058, 0.037, 0.008, -0.029, -0.058,
2047  3 -0.095, -0.124, -0.145, -0.175, -0.173, -0.163, -0.139, -0.099,
2048  4 -0.059, -0.011, 0.060, 0.138, 0.194, 0.234, 0.236, 0.176,
2049  5 0.085, -0.075, -0.304/
2050 ! s=1.7
2051  data (dty14(i),i= 1, 35)/
2052  1 0.056, 0.073, 0.082, 0.076, 0.086, 0.079, 0.081, 0.075,
2053  2 0.069, 0.063, 0.041, 0.012, 0.006, -0.030, -0.037, -0.073,
2054  3 -0.110, -0.124, -0.137, -0.152, -0.150, -0.141, -0.116, -0.068,
2055  4 -0.028, -0.011, 0.037, 0.077, 0.125, 0.157, 0.166, 0.130,
2056  5 0.039, -0.090, -0.304/
2057 ! effective s
2058 ! rs=1. - 1./(1. + exp(r-8.))
2059 ! si=s*( -0.0285 *log10(e0/100.)*rs + 1.)
2060  si = s
2061  if(si .lt. .3) then
2062  si=.4
2063  elseif(si .gt. 1.8) then
2064  si=1.7
2065  endif
2066  if(r .lt. 1.e-4) then
2067  ri=1.e-4
2068  elseif(r .gt. 70.) then
2069  ri=70.
2070  else
2071  ri=r
2072  endif
2073 !c if(ri .gt. 8.) then
2074 !c c=-3.5*(cosz-1.) + 1.
2075 !c ri=(ri-8.)*c + 8.
2076 !c endif
2077  ri=log10(ri)
2078 !
2079  call
2080  * k4ptdis(rat, 35, 14, 35, -3.80, 0.4, .158, .1, ri, si, ans)
2081  cf=10.**(ans)
e
dE dx *! Nuc Int sampling table e
Definition: cblkMuInt.h:130
ans
atmos%rho(atmos%nodes) **exp(-(z-atmos%z(atmos%nodes))/Hinf) elseif(z .lt. atmos%z(1)) then ans=atmos%rho(1) **exp((atmos%z(1) -z)/atmos%H(1)) else call kdwhereis(z, atmos%nodes, atmos%z, 1, i) a=atmos%a(i) if(a .ne. 0.d0) then ans=atmos%rho(i) **(1+a *(z-atmos%z(i))/atmos%H(i)) **(-1.0d0-1.d0/a) else ans=*atmos%rho(i) *exp(-(z-atmos%z(i))/atmos%H(i)) endif endif ! zsave=z ! endif cvh2den=ans end ! ---------------------------------- real *8 function cvh2temp(z) implicit none ! vettical height to temperatur(Kelvin) real *8 z ! input. vertical height in m ! output is temperature of the atmospher in Kelvin real *8 ans integer i if(z .gt. atmos%z(atmos%nodes)) then ans=atmos%T(atmos%nodes) elseif(z .lt. atmos%z(1)) then ans=atmos%T(1)+atmos%b(1) *(z - atmos%z(1)) else call kdwhereis(z, atmos%nodes, atmos%z, 1, i) ans=atmos%T(i)+atmos%b(i) *(z-atmos%z(i)) endif cvh2temp=ans end !--------------------------------------------- real *8 function cthick2h(t) implicit none real *8 t ! input. air thickness in kg/m^2 real *8 logt, ans integer i real *8 dod0, fd, a logt=log(t) if(t .ge. atmos%cumd(1)) then ans=atmos%z(1) - *(logt - atmos%logcumd(1)) *atmos%H(1) elseif(t .le. atmos%cumd(atmos%nodes)) then ans=atmos%z(atmos%nodes) - *Hinf *log(t/atmos%cumd(atmos%nodes)) else call kdwhereis(t, atmos%nodes, atmos%cumd, 1, i) ! i is such that X(i) > x >=x(i+1) ans
Definition: cstdatmos0.fNew2.h:82
r
*Zfirst p fm *Zfirst p Zfirst p Zfirst p *Zfirst p *Zfirst pos xyz r
Definition: ZavoidUnionMap.h:1
i
nodes i
Definition: cstdatmos0.fNew2.h:93
k4ptdis
subroutine k4ptdis(f, im, jm, iadj, x0, y0, hx, hy, x, y, ans)
Definition: genas.f:3533
Here is the call graph for this function:
Here is the caller graph for this function:

◆ kcfp()

subroutine kcfp (   e0,
  cosz,
  s,
  r,
  cf 
)

Definition at line 2111 of file genas.f.

References e, i, k4ptdis(), and r.

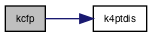
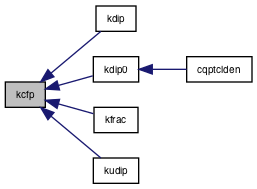
Referenced by kdip(), kdip0(), kfrac(), and kudip().

2111 ! e0: input. 1ry energy in tev.
2112 ! cosz: input. cos of zenith
2113 ! s: input. age of the proton shower
2114 ! for s<.5 or >1.6 not accurate.
2115 ! r: input. distance measured in moliere unit.
2116 ! moliere unit should be at 2r.l above the observation
2117 ! depth (along 1ry direction).
2118 ! cf: output. correction factor.
2119 ! cf*rho(s,r) gives normalized lateral distribution
2120 ! for particles giving de>0 in scinti.
2121 ! rho is the output from klee.
2122  dimension rat(35, 12)
2123  dimension dty1(35), dty2(35), dty3(35), dty4(35), dty5(35)
2124  dimension dty6(35), dty7(35), dty8(35), dty9(35), dty10(35)
2125  dimension dty11(35), dty12(35)
2126  equivalence(rat(1,1), dty1(1))
2127  equivalence(rat(1,2), dty2(1))
2128  equivalence(rat(1,3), dty3(1))
2129  equivalence(rat(1,4), dty4(1))
2130  equivalence(rat(1,5), dty5(1))
2131  equivalence(rat(1,6), dty6(1))
2132  equivalence(rat(1,7), dty7(1))
2133  equivalence(rat(1,8), dty8(1))
2134  equivalence(rat(1,9), dty9(1))
2135  equivalence(rat(1,10), dty10(1))
2136  equivalence(rat(1,11), dty11(1))
2137  equivalence(rat(1,12), dty12(1))
2138 ! proton fe.1sc3.5/lee s=.5
2139 ! rho*/rho=cf: log10(cf) for log10(r)=-3.84 to 1.6 step .16
2140 !
2141  data (dty1(i),i= 1, 35)/
2142 ! 1-1.3165,-1.2388,-1.1379,-1.0447,-0.8819,-0.6881,-0.5408,-0.3935,
2143  1-1.3565,-1.2388,-1.0579,-0.9047,-0.7819,-0.6481,-0.5108,-0.3935,
2144  2-0.3003,-0.2303,-0.1758,-0.1213,-0.0899,-0.0508,-0.0117, 0.0118,
2145 ! 3 0.0509, 0.0978, 0.1523, 0.2145, 0.2923, 0.4241, 0.5559, 0.7419,
2146  3 0.0509, 0.0978, 0.1523, 0.2145, 0.2923, 0.4241, 0.5559, 0.7119,
2147 ! 4 0.9279, 1.1680, 1.3772, 1.6096, 1.8574, 2.1130, 2.2139, 2.2530,
2148  4 0.9079, 1.0680, 1.2772, 1.5096, 1.7574, 2.0130, 2.1139, 2.1530,
2149 ! 5 2.2612, 2.2539, 2.2620/
2150  5 2.2012, 2.2239, 2.2320/
2151 ! s=.6
2152  data (dty2(i),i= 1, 35)/
2153  1 -1.10, -0.98, -0.82, -0.70, -0.60, -0.49, -0.39, -0.32,
2154  2 -0.24, -0.20, -0.15, -0.11, -0.08, -0.06, -0.05, -0.04,
2155  3 -0.02, 0.00, 0.03, 0.09, 0.17, 0.28, 0.36, 0.46,
2156  4 0.58, 0.72, 0.87, 1.03, 1.25, 1.48, 1.66, 1.90,
2157  5 2.08, 2.12, 2.12/
2158 ! s=.7
2159  data (dty3(i),i= 1, 35)/
2160  1 -1.05, -0.90, -0.78, -0.67, -0.55, -0.46, -0.38, -0.30,
2161  2 -0.25, -0.21, -0.19, -0.16, -0.14, -0.12, -0.10, -0.10,
2162  3 -0.07, -0.04, 0.01, 0.07, 0.12, 0.21, 0.29, 0.39,
2163  4 0.48, 0.60, 0.71, 0.84, 1.01, 1.18, 1.32, 1.48,
2164  5 1.58, 1.62, 1.64/
2165 ! s=0.8
2166  data (dty4(i),i= 1, 35)/
2167  1 -1.28, -1.20, -1.10, -0.94, -0.78, -0.61, -0.46, -0.36,
2168  2 -0.28, -0.24, -0.20, -0.17, -0.14, -0.14, -0.12, -0.12,
2169  3 -0.13, -0.09, -0.05, 0.00, 0.05, 0.12, 0.21, 0.29,
2170  4 0.38, 0.47, 0.57, 0.69, 0.81, 0.95, 1.06, 1.19,
2171  5 1.29, 1.37, 1.39/
2172 ! s=0.9
2173  data (dty5(i),i= 1, 35)/
2174  1 -1.28, -1.14, -1.08, -0.95, -0.80, -0.63, -0.50, -0.40,
2175  2 -0.32, -0.26, -0.24, -0.21, -0.20, -0.20, -0.19, -0.18,
2176  3 -0.16, -0.14, -0.10, -0.05, 0.00, 0.06, 0.11, 0.18,
2177  4 0.26, 0.35, 0.45, 0.55, 0.67, 0.82, 0.90, 0.98,
2178  5 1.03, 1.07, 1.07/
2179 ! s=1.0
2180  data (dty6(i),i= 1, 35)/
2181  1 -1.392, -1.260, -1.105, -0.926, -0.771, -0.616, -0.491, -0.398,
2182  2 -0.320, -0.272, -0.248, -0.216, -0.207, -0.191, -0.182, -0.181,
2183  3 -0.165, -0.156, -0.140, -0.108, -0.068, 0.002, 0.057, 0.120,
2184  4 0.198, 0.292, 0.377, 0.479, 0.596, 0.689, 0.752, 0.791,
2185  5 0.815, 0.793, 0.740/
2186 ! s=1.1
2187  data (dty7(i),i= 1, 35)/
2188  1 -1.26, -1.21, -1.11, -0.94, -0.80, -0.62, -0.51, -0.41,
2189  2 -0.30, -0.24, -0.20, -0.17, -0.15, -0.13, -0.11, -0.11,
2190  3 -0.10, -0.11, -0.10, -0.11, -0.09, -0.04, 0.01, 0.07,
2191  4 0.14, 0.23, 0.33, 0.42, 0.53, 0.60, 0.64, 0.62,
2192  5 0.59, 0.54, 0.45/
2193 ! s=1.2
2194  data (dty8(i),i= 1, 35)/
2195  1 -1.476, -1.391, -1.282, -1.073, -1.010, -0.816, -0.653, -0.506,
2196  2 -0.412, -0.326, -0.271, -0.216, -0.192, -0.176, -0.159, -0.151,
2197  3 -0.126, -0.125, -0.117, -0.100, -0.084, -0.060, -0.020, 0.043,
2198  4 0.105, 0.199, 0.277, 0.371, 0.441, 0.512, 0.544, 0.537,
2199  5 0.476, 0.369, 0.262/
2200 ! s=1.3
2201  data (dty9(i),i= 1, 35)/
2202  1 -1.507, -1.414, -1.351, -1.296, -1.126, -1.001, -0.877, -0.691,
2203  2 -0.536, -0.396, -0.310, -0.239, -0.177, -0.137, -0.098, -0.096,
2204  3 -0.103, -0.118, -0.124, -0.131, -0.099, -0.075, -0.035, 0.012,
2205  4 0.075, 0.160, 0.254, 0.332, 0.380, 0.442, 0.459, 0.413,
2206  5 0.322, 0.207, 0.116/
2207 ! s=1.4
2208  data (dty10(i),i= 1, 35)/
2209  1 -1.46, -1.38, -1.33, -1.30, -1.27, -1.17, -0.96, -0.83,
2210  2 -0.66, -0.52, -0.41, -0.31, -0.24, -0.20, -0.15, -0.15,
2211  3 -0.13, -0.13, -0.14, -0.13, -0.15, -0.12, -0.09, -0.04,
2212  4 0.02, 0.08, 0.17, 0.23, 0.29, 0.33, 0.32, 0.28,
2213  5 0.19, 0.07, -0.02/
2214 ! s=1.5
2215  data (dty11(i),i= 1, 35)/
2216  1 -1.63, -1.49, -1.44, -1.40, -1.38, -1.30,
2217  2 -1.21, -0.99, -0.83, -0.69, -0.53, -0.40, -0.29, -0.23,
2218  3 -0.17, -0.14, -0.14, -0.13, -0.16, -0.19, -0.19, -0.18,
2219  4 -0.15, -0.11, -0.06, -0.01, 0.05, 0.12, 0.18, 0.23,
2220  5 0.21, 0.16, 0.06, -0.05, -0.13/
2221 ! s=1.6
2222  data (dty12(i),i= 1, 35)/
2223  1 -1.46, -1.45, -1.43, -1.43, -1.40, -1.34, -1.27, -1.19,
2224  2 -1.02, -0.85, -0.68, -0.54, -0.40, -0.29, -0.23, -0.18,
2225  3 -0.16, -0.16, -0.17, -0.19, -0.20, -0.18, -0.16, -0.14,
2226  4 -0.11, -0.06, 0.02, 0.07, 0.11, 0.12, 0.10, 0.03,
2227  5 -0.07, -0.14, -0.20/
2228 !
2229 ! effective s
2230 !c rs=1. - 1./(1. + exp(r-8.))
2231 !c si=s*( -0.0285 *log10(e0/100.)*rs + 1.)
2232  si = s
2233  if(si .lt. .4) then
2234  si=.4
2235  elseif(si .gt. 1.7) then
2236  si=1.7
2237  endif
2238  if(r .lt. 1.e-4) then
2239  ri=1.e-4
2240  elseif(r .gt. 70.) then
2241  ri=70.
2242  else
2243  ri=r
2244  endif
2245 !c if(ri .gt. 8.) then
2246 !c c=-3.5*(cosz-1.) + 1.
2247 !c ri=(ri-8.)*c + 8.
2248 !c endif
2249  ri=log10(ri)
2250 !
2251  call
2252  * k4ptdis(rat, 35, 12, 35, -3.84, 0.5, .16, .1, ri, si, ans)
2253  cf=10.**(ans)
e
dE dx *! Nuc Int sampling table e
Definition: cblkMuInt.h:130
ans
atmos%rho(atmos%nodes) **exp(-(z-atmos%z(atmos%nodes))/Hinf) elseif(z .lt. atmos%z(1)) then ans=atmos%rho(1) **exp((atmos%z(1) -z)/atmos%H(1)) else call kdwhereis(z, atmos%nodes, atmos%z, 1, i) a=atmos%a(i) if(a .ne. 0.d0) then ans=atmos%rho(i) **(1+a *(z-atmos%z(i))/atmos%H(i)) **(-1.0d0-1.d0/a) else ans=*atmos%rho(i) *exp(-(z-atmos%z(i))/atmos%H(i)) endif endif ! zsave=z ! endif cvh2den=ans end ! ---------------------------------- real *8 function cvh2temp(z) implicit none ! vettical height to temperatur(Kelvin) real *8 z ! input. vertical height in m ! output is temperature of the atmospher in Kelvin real *8 ans integer i if(z .gt. atmos%z(atmos%nodes)) then ans=atmos%T(atmos%nodes) elseif(z .lt. atmos%z(1)) then ans=atmos%T(1)+atmos%b(1) *(z - atmos%z(1)) else call kdwhereis(z, atmos%nodes, atmos%z, 1, i) ans=atmos%T(i)+atmos%b(i) *(z-atmos%z(i)) endif cvh2temp=ans end !--------------------------------------------- real *8 function cthick2h(t) implicit none real *8 t ! input. air thickness in kg/m^2 real *8 logt, ans integer i real *8 dod0, fd, a logt=log(t) if(t .ge. atmos%cumd(1)) then ans=atmos%z(1) - *(logt - atmos%logcumd(1)) *atmos%H(1) elseif(t .le. atmos%cumd(atmos%nodes)) then ans=atmos%z(atmos%nodes) - *Hinf *log(t/atmos%cumd(atmos%nodes)) else call kdwhereis(t, atmos%nodes, atmos%cumd, 1, i) ! i is such that X(i) > x >=x(i+1) ans
Definition: cstdatmos0.fNew2.h:82
r
*Zfirst p fm *Zfirst p Zfirst p Zfirst p *Zfirst p *Zfirst pos xyz r
Definition: ZavoidUnionMap.h:1
i
nodes i
Definition: cstdatmos0.fNew2.h:93
k4ptdis
subroutine k4ptdis(f, im, jm, iadj, x0, y0, hx, hy, x, y, ans)
Definition: genas.f:3533
Here is the call graph for this function:
Here is the caller graph for this function:

◆ kcfpb()

subroutine kcfpb (   e0,
  cosz,
  s,
  r,
  cf 
)

Definition at line 2280 of file genas.f.

References e, i, k4ptdis(), and r.

Referenced by kdipb(), kdipb0(), kfrac(), and kudipb().

2280 ! e0: input. 1ry energy in tev.
2281 ! at present not used.
2282 ! cosz: input. cos of zenith
2283 ! s: input. age of the proton shower
2284 ! for s<.4 or >1.7 not accurate.
2285 ! r: input. distance measured in moliere unit.
2286 ! moliere unit should be at 2r.l above the observation
2287 ! depth (along 1ry direction).
2288 ! cf: output. correction factor.
2289 ! cf*rho(s,r) gives normalized lateral distribution
2290 ! for particles giving de>0 in scinti.
2291 ! rho is the output from klee.
2292  dimension rat(35, 13)
2293  dimension dty1(35), dty2(35), dty3(35), dty4(35), dty5(35)
2294  dimension dty6(35), dty7(35), dty8(35), dty9(35), dty10(35)
2295  dimension dty11(35), dty12(35), dty13(35)
2296  equivalence(rat(1,1), dty1(1))
2297  equivalence(rat(1,2), dty2(1))
2298  equivalence(rat(1,3), dty3(1))
2299  equivalence(rat(1,4), dty4(1))
2300  equivalence(rat(1,5), dty5(1))
2301  equivalence(rat(1,6), dty6(1))
2302  equivalence(rat(1,7), dty7(1))
2303  equivalence(rat(1,8), dty8(1))
2304  equivalence(rat(1,9), dty9(1))
2305  equivalence(rat(1,10), dty10(1))
2306  equivalence(rat(1,11), dty11(1))
2307  equivalence(rat(1,12), dty12(1))
2308  equivalence(rat(1,13), dty13(1))
2309 ! rho*/rho=cf: log10(cf) for log10(r)=-3.84 to 1.6 step .16
2310 ! proton 10**14 ev rho(pb.5fe.1sc3.5)/lee s=0.4
2311  data (dty1(i),i= 1, 35)/
2312  1 -1.398, -1.320, -1.176, -1.020, -0.905, -0.761, -0.641, -0.545,
2313  2 -0.461, -0.383, -0.335, -0.275, -0.221, -0.173, -0.107, -0.065,
2314  3 -0.023, 0.014, 0.074, 0.224, 0.368, 0.542, 0.734, 0.884,
2315  4 1.071, 1.245, 1.401, 1.635, 1.809, 1.947, 2.068, 2.116,
2316  5 2.152, 2.152, 2.158/
2317 ! s=0.5
2318  data (dty2(i),i= 1, 35)/
2319  1 -1.002, -0.857, -0.725, -0.647, -0.575, -0.515, -0.461, -0.407,
2320  2 -0.359, -0.317, -0.263, -0.215, -0.149, -0.095, -0.047, -0.017,
2321  3 -0.011, -0.005, 0.026, 0.116, 0.212, 0.368, 0.512, 0.668,
2322  4 0.818, 0.992, 1.155, 1.323, 1.491, 1.611, 1.725, 1.809,
2323  5 1.839, 1.857, 1.863/
2324 ! s=0.6
2325  data (dty3(i),i= 1, 35)/
2326  1 -0.899, -0.779, -0.677, -0.575, -0.473, -0.395, -0.329, -0.287,
2327  2 -0.227, -0.185, -0.131, -0.107, -0.077, -0.047, -0.029, -0.023,
2328  3 -0.017, -0.011, 0.008, 0.044, 0.074, 0.128, 0.230, 0.350,
2329  4 0.500, 0.686, 0.872, 1.047, 1.209, 1.341, 1.449, 1.551,
2330  5 1.629, 1.659, 1.665/
2331 ! s=0.7
2332  data (dty4(i),i= 1, 35)/
2333  1 -0.917, -0.743, -0.617, -0.503, -0.389, -0.293, -0.209, -0.149,
2334  2 -0.089, -0.053, -0.035, -0.023, -0.035, -0.041, -0.047, -0.065,
2335  3 -0.065, -0.053, -0.041, -0.017, 0.020, 0.080, 0.164, 0.296,
2336  4 0.422, 0.578, 0.728, 0.878, 1.059, 1.197, 1.323, 1.425,
2337  5 1.509, 1.551, 1.551/
2338 ! s=0.8
2339  data (dty5(i),i= 1, 35)/
2340  1 -0.881, -0.749, -0.623, -0.503, -0.395, -0.311, -0.233, -0.167,
2341  2 -0.119, -0.089, -0.065, -0.059, -0.059, -0.065, -0.065, -0.077,
2342  3 -0.083, -0.107, -0.107, -0.089, -0.041, 0.038, 0.092, 0.176,
2343  4 0.266, 0.386, 0.518, 0.644, 0.806, 0.998, 1.137, 1.263,
2344  5 1.341, 1.353, 1.365/
2345 ! s=.9
2346  data (dty6(i),i= 1, 35)/
2347  1 -1.194, -1.008, -0.833, -0.647, -0.497, -0.365, -0.269, -0.191,
2348  2 -0.125, -0.083, -0.053, -0.053, -0.047, -0.059, -0.077, -0.083,
2349  3 -0.077, -0.077, -0.089, -0.107, -0.095, -0.053, 0.008, 0.098,
2350  4 0.182, 0.284, 0.386, 0.500, 0.602, 0.716, 0.830, 0.920,
2351  5 1.005, 1.059, 1.065/
2352 ! s=1.0
2353  data (dty7(i),i= 1, 35)/
2354  1 -1.386, -1.218, -1.014, -0.827, -0.641, -0.485, -0.359, -0.251,
2355  2 -0.173, -0.107, -0.071, -0.041, -0.047, -0.047, -0.065, -0.071,
2356  3 -0.077, -0.089, -0.101, -0.113, -0.107, -0.083, -0.035, 0.026,
2357  4 0.116, 0.212, 0.338, 0.458, 0.542, 0.608, 0.656, 0.698,
2358  5 0.728, 0.752, 0.758/
2359 ! s=1.1
2360  data (dty8(i),i= 1, 35)/
2361  1 -1.386, -1.188, -1.020, -0.821, -0.635, -0.491, -0.371, -0.269,
2362  2 -0.197, -0.137, -0.095, -0.065, -0.047, -0.053, -0.065, -0.077,
2363  3 -0.095, -0.107, -0.113, -0.125, -0.113, -0.089, -0.053, 0.002,
2364  4 0.074, 0.176, 0.272, 0.362, 0.458, 0.518, 0.554, 0.566,
2365  5 0.554, 0.500, 0.410/
2366 ! s=1.2
2367  data (dty9(i),i= 1, 35)/
2368  1 -1.404, -1.284, -1.152, -0.977, -0.797, -0.635, -0.473, -0.365,
2369  2 -0.263, -0.185, -0.125, -0.095, -0.071, -0.065, -0.077, -0.089,
2370  3 -0.095, -0.101, -0.107, -0.119, -0.119, -0.107, -0.083, -0.029,
2371  4 0.038, 0.098, 0.188, 0.284, 0.362, 0.434, 0.458, 0.446,
2372  5 0.416, 0.326, 0.194/
2373 ! s=1.3
2374  data (dty10(i),i= 1, 35)/
2375  1 -1.398, -1.344, -1.295, -1.163, -0.953, -0.744, -0.581, -0.425,
2376  2 -0.317, -0.233, -0.173, -0.143, -0.125, -0.112, -0.118, -0.118,
2377  3 -0.117, -0.123, -0.135, -0.140, -0.140, -0.128, -0.115, -0.067,
2378  4 -0.007, 0.065, 0.143, 0.216, 0.294, 0.348, 0.360, 0.325,
2379  5 0.253, 0.158, 0.026/
2380 ! s=1.4
2381  data (dty11(i),i= 1, 35)/
2382  1 -1.470, -1.391, -1.307, -1.205, -1.031, -0.863, -0.713, -0.557,
2383  2 -0.413, -0.305, -0.215, -0.161, -0.125, -0.106, -0.094, -0.100,
2384  3 -0.105, -0.111, -0.117, -0.140, -0.128, -0.110, -0.097, -0.079,
2385  4 -0.013, 0.035, 0.107, 0.192, 0.270, 0.294, 0.288, 0.253,
2386  5 0.181, 0.050, -0.082/
2387 ! s=1.5
2388  data (dty12(i),i= 1, 35)/
2389  1 -1.446, -1.355, -1.295, -1.247, -1.163, -1.073, -0.875, -0.659,
2390  2 -0.485, -0.347, -0.257, -0.191, -0.142, -0.112, -0.112, -0.106,
2391  3 -0.111, -0.117, -0.135, -0.140, -0.134, -0.128, -0.103, -0.067,
2392  4 -0.019, 0.017, 0.066, 0.168, 0.216, 0.246, 0.234, 0.181,
2393  5 0.091, -0.058, -0.201/
2394 ! s=1.6
2395  data (dty13(i),i= 1, 35)/
2396  1 -1.559, -1.499, -1.445, -1.403, -1.307, -1.217, -1.084, -0.749,
2397  2 -0.533, -0.395, -0.305, -0.227, -0.184, -0.154, -0.142, -0.160,
2398  3 -0.153, -0.165, -0.165, -0.158, -0.158, -0.152, -0.127, -0.097,
2399  4 -0.055, -0.001, 0.060, 0.108, 0.162, 0.210, 0.205, 0.151,
2400  5 0.050, -0.106, -0.297/
2401 ! effective s
2402 !c rs=1. - 1./(1. + exp(r-8.))
2403 !c si=s*( -0.0285 *log10(e0/100.)*rs + 1.)
2404  si = s
2405  if(si .lt. .3) then
2406  si=.3
2407  elseif(si .gt. 1.7) then
2408  si=1.7
2409  endif
2410  if(r .lt. 1.e-4) then
2411  ri=1.e-4
2412  elseif(r .gt. 70.) then
2413  ri=70.
2414  else
2415  ri=r
2416  endif
2417 !c if(ri .gt. 8.) then
2418 !c c=-3.5*(cosz-1.) + 1.
2419 !c ri=(ri-8.)*c + 8.
2420 !c endif
2421  ri=log10(ri)
2422 !
2423  call
2424  * k4ptdis(rat, 35, 13, 35, -3.80, 0.4, .158, .1, ri, si, ans)
2425  cf=10.**(ans)
e
dE dx *! Nuc Int sampling table e
Definition: cblkMuInt.h:130
ans
atmos%rho(atmos%nodes) **exp(-(z-atmos%z(atmos%nodes))/Hinf) elseif(z .lt. atmos%z(1)) then ans=atmos%rho(1) **exp((atmos%z(1) -z)/atmos%H(1)) else call kdwhereis(z, atmos%nodes, atmos%z, 1, i) a=atmos%a(i) if(a .ne. 0.d0) then ans=atmos%rho(i) **(1+a *(z-atmos%z(i))/atmos%H(i)) **(-1.0d0-1.d0/a) else ans=*atmos%rho(i) *exp(-(z-atmos%z(i))/atmos%H(i)) endif endif ! zsave=z ! endif cvh2den=ans end ! ---------------------------------- real *8 function cvh2temp(z) implicit none ! vettical height to temperatur(Kelvin) real *8 z ! input. vertical height in m ! output is temperature of the atmospher in Kelvin real *8 ans integer i if(z .gt. atmos%z(atmos%nodes)) then ans=atmos%T(atmos%nodes) elseif(z .lt. atmos%z(1)) then ans=atmos%T(1)+atmos%b(1) *(z - atmos%z(1)) else call kdwhereis(z, atmos%nodes, atmos%z, 1, i) ans=atmos%T(i)+atmos%b(i) *(z-atmos%z(i)) endif cvh2temp=ans end !--------------------------------------------- real *8 function cthick2h(t) implicit none real *8 t ! input. air thickness in kg/m^2 real *8 logt, ans integer i real *8 dod0, fd, a logt=log(t) if(t .ge. atmos%cumd(1)) then ans=atmos%z(1) - *(logt - atmos%logcumd(1)) *atmos%H(1) elseif(t .le. atmos%cumd(atmos%nodes)) then ans=atmos%z(atmos%nodes) - *Hinf *log(t/atmos%cumd(atmos%nodes)) else call kdwhereis(t, atmos%nodes, atmos%cumd, 1, i) ! i is such that X(i) > x >=x(i+1) ans
Definition: cstdatmos0.fNew2.h:82
r
*Zfirst p fm *Zfirst p Zfirst p Zfirst p *Zfirst p *Zfirst pos xyz r
Definition: ZavoidUnionMap.h:1
i
nodes i
Definition: cstdatmos0.fNew2.h:93
k4ptdis
subroutine k4ptdis(f, im, jm, iadj, x0, y0, hx, hy, x, y, ans)
Definition: genas.f:3533
Here is the call graph for this function:
Here is the caller graph for this function:

◆ kdig()

subroutine kdig (   e0,
  zob,
  cosz,
  s,
  de,
  j1,
  r,
  rho 
)

Definition at line 2460 of file genas.f.

References kcfg(), kide(), klee(), knrml(), and r.

2460 !
2461  external kcfg, kide
2462  if(j1 .eq. 0) then
2463  call knrml(e0, zob, cosz, s, de, kcfg, kide, sum)
2464  endif
2465  call klee(s, r, rhone)
2466  call kcfg(e0, cosz, s, r, cf)
2467  call kide(e0, zob, s, cosz, j1, r, de, fr)
2468  rho=rhone*cf*fr/sum
kide
subroutine kide(e0, zob, s, cosz, j1, rr, de, fr)
Definition: genas.f:2665
r
*Zfirst p fm *Zfirst p Zfirst p Zfirst p *Zfirst p *Zfirst pos xyz r
Definition: ZavoidUnionMap.h:1
klee
subroutine klee(s, r, rho)
kklibg >>>>>>>>>>>>>>>>>>>>>>>>>>>>
Definition: genas.f:3552
knrml
subroutine knrml(e0, zob, cosz, s, de, kcfx, kidx, sum)
Definition: genas.f:3603
kcfg
subroutine kcfg(e0, cosz, s, r, cf)
Definition: genas.f:1765
Here is the call graph for this function:

◆ kdig0()

subroutine kdig0 (   e0,
  cosz,
  s,
  r,
  rho 
)

Definition at line 1622 of file genas.f.

References kcfg(), klee(), and r.

Referenced by cqptclden().

1622 !
1623  call klee(s, r, rhone)
1624  call kcfg(e0, cosz, s, r, cf)
1625  rho=rhone*cf
r
*Zfirst p fm *Zfirst p Zfirst p Zfirst p *Zfirst p *Zfirst pos xyz r
Definition: ZavoidUnionMap.h:1
klee
subroutine klee(s, r, rho)
kklibg >>>>>>>>>>>>>>>>>>>>>>>>>>>>
Definition: genas.f:3552
kcfg
subroutine kcfg(e0, cosz, s, r, cf)
Definition: genas.f:1765
Here is the call graph for this function:
Here is the caller graph for this function:

◆ kdigb()

subroutine kdigb (   e0,
  zob,
  cosz,
  s,
  de,
  j1,
  r,
  rho 
)

Definition at line 2510 of file genas.f.

References kcfgb(), kideb(), klee(), knrml(), and r.

2510 !
2511  external kcfgb, kideb
2512  if(j1 .eq. 0) then
2513  call knrml(e0, zob, cosz, s, de, kcfgb, kideb, sum)
2514  endif
2515  call klee(s, r, rhone)
2516  call kcfgb(e0, cosz, s, r, cf)
2517  call kideb(e0, zob, s, cosz, j1, r, de, fr)
2518  rho=rhone*cf*fr/sum
r
*Zfirst p fm *Zfirst p Zfirst p Zfirst p *Zfirst p *Zfirst pos xyz r
Definition: ZavoidUnionMap.h:1
klee
subroutine klee(s, r, rho)
kklibg >>>>>>>>>>>>>>>>>>>>>>>>>>>>
Definition: genas.f:3552
kideb
subroutine kideb(e0, zob, s, cosz, j1, rr, de, fr)
Definition: genas.f:2728
knrml
subroutine knrml(e0, zob, cosz, s, de, kcfx, kidx, sum)
Definition: genas.f:3603
kcfgb
subroutine kcfgb(e0, cosz, s, r, cf)
Definition: genas.f:1927
Here is the call graph for this function:

◆ kdigb0()

subroutine kdigb0 (   e0,
  cosz,
  s,
  r,
  rho 
)

Definition at line 1615 of file genas.f.

References kcfgb(), klee(), and r.

Referenced by cqptclden().

1615 !
1616  call klee(s, r, rhone)
1617  call kcfgb(e0, cosz, s, r, cf)
1618  rho=rhone*cf
r
*Zfirst p fm *Zfirst p Zfirst p Zfirst p *Zfirst p *Zfirst pos xyz r
Definition: ZavoidUnionMap.h:1
klee
subroutine klee(s, r, rho)
kklibg >>>>>>>>>>>>>>>>>>>>>>>>>>>>
Definition: genas.f:3552
kcfgb
subroutine kcfgb(e0, cosz, s, r, cf)
Definition: genas.f:1927
Here is the call graph for this function:
Here is the caller graph for this function:

◆ kdip()

subroutine kdip (   e0,
  zob,
  cosz,
  s,
  de,
  j1,
  r,
  rho 
)

Definition at line 2472 of file genas.f.

References kcfp(), kide(), klee(), knrml(), and r.

2472  external kcfp, kide
2473  if(j1 .eq. 0) then
2474  call knrml(e0, zob, cosz, s, de, kcfp, kide, sum)
2475  endif
2476  call klee(s, r, rhone)
2477  call kcfp(e0, cosz, s, r, cf)
2478  call kide(e0, zob, s, cosz, j1, r, de, fr)
2479  rho=rhone*cf*fr/sum
kide
subroutine kide(e0, zob, s, cosz, j1, rr, de, fr)
Definition: genas.f:2665
r
*Zfirst p fm *Zfirst p Zfirst p Zfirst p *Zfirst p *Zfirst pos xyz r
Definition: ZavoidUnionMap.h:1
klee
subroutine klee(s, r, rho)
kklibg >>>>>>>>>>>>>>>>>>>>>>>>>>>>
Definition: genas.f:3552
knrml
subroutine knrml(e0, zob, cosz, s, de, kcfx, kidx, sum)
Definition: genas.f:3603
kcfp
subroutine kcfp(e0, cosz, s, r, cf)
Definition: genas.f:2111
Here is the call graph for this function:

◆ kdip0()

subroutine kdip0 (   e0,
  cosz,
  s,
  r,
  rho 
)

Definition at line 1636 of file genas.f.

References kcfp(), klee(), and r.

Referenced by cqptclden().

1636 !
1637  call klee(s, r, rhone)
1638  call kcfp(e0, cosz, s, r, cf)
1639  rho=rhone*cf
r
*Zfirst p fm *Zfirst p Zfirst p Zfirst p *Zfirst p *Zfirst pos xyz r
Definition: ZavoidUnionMap.h:1
klee
subroutine klee(s, r, rho)
kklibg >>>>>>>>>>>>>>>>>>>>>>>>>>>>
Definition: genas.f:3552
kcfp
subroutine kcfp(e0, cosz, s, r, cf)
Definition: genas.f:2111
Here is the call graph for this function:
Here is the caller graph for this function:

◆ kdipb()

subroutine kdipb (   e0,
  zob,
  cosz,
  s,
  de,
  j1,
  r,
  rho 
)

Definition at line 2522 of file genas.f.

References kcfpb(), kideb(), klee(), knrml(), and r.

2522  external kcfpb, kideb
2523  if(j1 .eq. 0) then
2524  call knrml(e0, zob, cosz, s, de, kcfpb, kideb, sum)
2525  endif
2526  call klee(s, r, rhone)
2527  call kcfpb(e0, cosz, s, r, cf)
2528  call kideb(e0, zob, s, cosz, j1, r, de, fr)
2529  rho=rhone*cf*fr/sum
r
*Zfirst p fm *Zfirst p Zfirst p Zfirst p *Zfirst p *Zfirst pos xyz r
Definition: ZavoidUnionMap.h:1
klee
subroutine klee(s, r, rho)
kklibg >>>>>>>>>>>>>>>>>>>>>>>>>>>>
Definition: genas.f:3552
kideb
subroutine kideb(e0, zob, s, cosz, j1, rr, de, fr)
Definition: genas.f:2728
knrml
subroutine knrml(e0, zob, cosz, s, de, kcfx, kidx, sum)
Definition: genas.f:3603
kcfpb
subroutine kcfpb(e0, cosz, s, r, cf)
Definition: genas.f:2280
Here is the call graph for this function:

◆ kdipb0()

subroutine kdipb0 (   e0,
  cosz,
  s,
  r,
  rho 
)

Definition at line 1629 of file genas.f.

References kcfpb(), klee(), and r.

Referenced by cqptclden().

1629 !
1630  call klee(s, r, rhone)
1631  call kcfpb(e0, cosz, s, r, cf)
1632  rho=rhone*cf
r
*Zfirst p fm *Zfirst p Zfirst p Zfirst p *Zfirst p *Zfirst pos xyz r
Definition: ZavoidUnionMap.h:1
klee
subroutine klee(s, r, rho)
kklibg >>>>>>>>>>>>>>>>>>>>>>>>>>>>
Definition: genas.f:3552
kcfpb
subroutine kcfpb(e0, cosz, s, r, cf)
Definition: genas.f:2280
Here is the call graph for this function:
Here is the caller graph for this function:

◆ kefg()

subroutine kefg (   cosz,
  s,
  ef 
)

Definition at line 2556 of file genas.f.

References r.

2556 ! for cosz=1.
2557  r= 1.012 + .4645*s
2558 ! cosz correction (verified upto cos=.7)
2559 ! for s< 1. should be examined.)
2560  ef=1. + (r-1.)/cosz
r
*Zfirst p fm *Zfirst p Zfirst p Zfirst p *Zfirst p *Zfirst pos xyz r
Definition: ZavoidUnionMap.h:1

◆ kefgb()

subroutine kefgb (   cosz,
  s,
  ef 
)

Definition at line 2594 of file genas.f.

References r.

2594 ! for cosz=1.
2595  r=( .383*s -0.1389)*s + 1.79
2596 ! cosz correction ( verified uptp cos=0.7)
2597  ef=1. - (1.-cosz)* 0.575 + (r-1.)/cosz
r
*Zfirst p fm *Zfirst p Zfirst p Zfirst p *Zfirst p *Zfirst pos xyz r
Definition: ZavoidUnionMap.h:1

◆ kefp()

subroutine kefp (   cosz,
  s,
  ef 
)

Definition at line 2563 of file genas.f.

References r.

2563 ! use same as kefg
2564 ! for cosz=1.
2565  r= 1.012 + .4645*s
2566 ! cosz correction
2567 ! for s< 1. should be examined.)
2568  ef=1. + (r-1.)/cosz
r
*Zfirst p fm *Zfirst p Zfirst p Zfirst p *Zfirst p *Zfirst pos xyz r
Definition: ZavoidUnionMap.h:1

◆ kefpb()

subroutine kefpb (   cosz,
  s,
  ef 
)

Definition at line 2600 of file genas.f.

References r.

2600 ! use same as kefgb
2601 ! for cosz=1.
2602  r=( .383*s -0.1389)*s + 1.79
2603 ! cosz correction
2604  ef=1. - (1.-cosz)* 0.575 + (r-1.)/cosz
r
*Zfirst p fm *Zfirst p Zfirst p Zfirst p *Zfirst p *Zfirst pos xyz r
Definition: ZavoidUnionMap.h:1

◆ kfrac()

subroutine kfrac (   jsc,
  k,
  e0,
  zob,
  cosz,
  s,
  pmin,
  frac 
)

Definition at line 2628 of file genas.f.

References kcfg(), kcfgb(), kcfp(), kcfpb(), kide(), kideb(), and knrml().

2628  include "Zascns"
2629  external kcfp, kide
2630  external kcfg, kcfpb
2631  external kcfgb, kideb
2632  if(pmin .eq. 0.) then
2633  frac=1.
2634  else
2635  if(jsc .eq. 1) then
2636 ! fe.1sc3.5
2637  demin=pmin*eqvo1
2638  if(k .eq. 0) then
2639  call knrml(e0, zob, cosz, s, demin, kcfg,
2640  * kide, frac )
2641  elseif(k .eq. 1) then
2642  call knrml(e0, zob, cosz, s, demin, kcfp,
2643  * kide, frac )
2644  endif
2645  elseif(jsc .eq. 2) then
2646  demin=pmin*eqvo2
2647  if(k .eq. 0) then
2648  call knrml(e0, zob, cosz, s, demin, kcfgb,
2649  * kideb, frac )
2650  elseif(k .eq. 1) then
2651  call knrml(e0, zob, cosz, s, demin, kcfpb,
2652  * kideb, frac )
2653  endif
2654  endif
2655  endif
kide
subroutine kide(e0, zob, s, cosz, j1, rr, de, fr)
Definition: genas.f:2665
kideb
subroutine kideb(e0, zob, s, cosz, j1, rr, de, fr)
Definition: genas.f:2728
knrml
subroutine knrml(e0, zob, cosz, s, de, kcfx, kidx, sum)
Definition: genas.f:3603
kcfg
subroutine kcfg(e0, cosz, s, r, cf)
Definition: genas.f:1765
kcfpb
subroutine kcfpb(e0, cosz, s, r, cf)
Definition: genas.f:2280
kcfgb
subroutine kcfgb(e0, cosz, s, r, cf)
Definition: genas.f:1927
kcfp
subroutine kcfp(e0, cosz, s, r, cf)
Definition: genas.f:2111
Here is the call graph for this function:

◆ kfrges()

subroutine kfrges ( dimension(intvx, *)  x,
  intvx,
  n,
  c,
  m,
  icon 
)

Definition at line 3434 of file genas.f.

References c, i, m, n, and x.

Referenced by kide1(), kide2(), kide3(), kideb1(), kideb2(), and kideb3().

3434 !
3435 ! dimension x(intvx, n)
3436 ! ( , *) is to avoid possible warning at debug time
3437  dimension x(intvx, *)
3438 !
3439  if( n .gt. 0 ) then
3440  do 10 i=1, n
3441  if(x(1,i) .ge. c) then
3442  m=i
3443  icon=0
3444  goto 100
3445  endif
3446  10 continue
3447  icon=1
3448  m=n+1
3449  elseif(n .lt. 0) then
3450  do 20 i=-n, 1, -1
3451  if(x(1,i) .ge. c) then
3452  m=i
3453  icon=0
3454  goto 100
3455  endif
3456  20 continue
3457  m=0
3458  icon=1
3459  else
3460  icon=1
3461  endif
3462  100 continue
i
nodes i
Definition: cstdatmos0.fNew2.h:93
m
block data include Zlatfit h c fitting region data data data data data d0 data data d0 data data m
Definition: ZlatfitBD.h:35
n
integer n
Definition: Zcinippxc.h:1
x
! structure defining a particle at production ! Basic idea of what is to be contained in ! the particle structue is that dynamical ones should be included those derivable from the particle code ! is not included ******************************************************type fmom momentum sequence union map real e endmap map real * x
Definition: Zptcl.h:21
c
dE dx *! Nuc Int sampling table c
Definition: cblkMuInt.h:130
Here is the caller graph for this function:

◆ kgausss()

subroutine kgausss (   av,
  s,
  x1,
  x2 
)

Definition at line 3489 of file genas.f.

References rndcsng(), x1(), and x2().

3489 !
3490 !
3491 ! ..... do until ....
3492  20 continue
3493  call rndcsng(u1)
3494  call rndcsng(u2)
3495 ! generate cos(p) and sin(p)
3496  u1=u1+u1-1.
3497  u1s=u1*u1
3498  u2s=u2*u2
3499  tmp=u1s+u2s
3500  if(.not.
3501  * (tmp .lt. 1.)
3502  * ) goto 20
3503 ! ... end until ...
3504  call rndcsng(u3)
3505  al=alog(u3)
3506  al=sqrt(-al-al)
3507  cs=(u1s-u2s)/tmp
3508  sn=u1*u2/tmp
3509  sn=sn+sn
3510  x1=al*cs*s+av
3511  x2=al*sn*s+av
x1
block data include Zlatfit h c fitting region data x1(1)/0.03/
rndcsng
subroutine rndcsng(u)
Definition: genas.f:33
nrl_atmos::al
real(4), save al
Definition: cNRLAtmos.f:22
x2
block data include Zlatfit h c fitting region data x2(1)/0.5/data x1(2)/0.3/
Here is the call graph for this function:

◆ kide()

subroutine kide (   e0,
  zob,
  s,
  cosz,
  j1,
  rr,
  de,
  fr 
)

Definition at line 2665 of file genas.f.

References kide1(), kide2(), kide3(), kmolu(), r, stzss(), and z.

Referenced by kdig(), kdip(), kfrac(), kudig(), and kudip().

2665 ! e0: input. 1ry energy of gamma in tev
2666 ! zob: input. observation depth (g/cm**2) (vetical)
2667 ! s: input. age of the shower
2668 ! cosz: input. cos of the zenith angle of the shower
2669 ! j1: input. 0--> some of the above parameters are not equal to
2670 ! those in previous call.
2671 ! ^=0-->all above parameters are equal to those
2672 ! in the previous call.
2673 ! de: input. energy deposit in scintillater. in mev
2674 ! rr: input. distance from the core in m
2675 ! fr: output. fraction of particles > de at r.
2676 !
2677  include "Zascns"
2678  data ssave/5./
2679  save ssave, rcnv, um1, um2
2680 !
2681  if(j1 .eq. 0) then
2682 ! new parameters
2683  if(abs(s/ssave-1.) .gt. smarg) then
2684  ssave=s
2685 ! um1=m.u (2 r.l above the observation depht,
2686 ! along the 1ry direction) (in m)
2687  call kmolu(zob, cosz, um1)
2688 ! um2=m.u (same as above) for the depth where
2689 ! the standard shower takes the same age (=s) as the
2690 ! currently considered shower.
2691  call stzss(s, z)
2692  call kmolu(z, cosz, um2)
2693 ! ssmu is in Zascns (standard shower m.u)
2694  rcnv= sqrt( ssmu * um2)/um1
2695  endif
2696  endif
2697  if(de .gt. 0.) then
2698 ! effective r
2699  r=rr* rcnv
2700  if(e0 .lt. .1) then
2701  r=r+10.
2702  endif
2703  if(cosz .gt. .9) then
2704 ! use vertical one
2705  deo=de*cosz
2706  call kide1(deo, r, fr)
2707  elseif(cosz .gt. .75) then
2708 ! use cos=0.8
2709  deo=de*cosz/0.8
2710  call kide2(deo, r, fr)
2711  else
2712 ! use cos=.7
2713  deo=de*cosz/0.7
2714  call kide3(deo, r, fr)
2715  endif
2716  else
2717  fr=1.
2718  endif
z
nodes z
Definition: cstdatmos0.fNew2.h:93
r
*Zfirst p fm *Zfirst p Zfirst p Zfirst p *Zfirst p *Zfirst pos xyz r
Definition: ZavoidUnionMap.h:1
kmolu
subroutine kmolu(dep, cosz, rmu)
Definition: genas.f:3583
kide3
subroutine kide3(de, r, fr)
Definition: genas.f:3271
kide2
subroutine kide2(de, r, fr)
Definition: genas.f:3173
stzss
subroutine stzss(S, Z)
Definition: genas.f:3713
kide1
subroutine kide1(de, r, fr)
Definition: genas.f:3074
Here is the call graph for this function:
Here is the caller graph for this function:

◆ kide1()

subroutine kide1 (   de,
  r,
  fr 
)

Definition at line 3074 of file genas.f.

References j, kfrges(), and r.

Referenced by kide().

3074 ! de: input. energy deposit in scintillater. in mev
3075 ! r: input. distance from the core in m
3076 ! fr: output. fraction of particles > de at r.
3077 !
3078  include "Zdeg"
3079 !
3080 !
3081  if(r .gt. 1780.) then
3082 ! better not to use r>1780
3083  rr=1333.
3084  else
3085  rr=r
3086  endif
3087  if(rr .lt. 15.) then
3088  j=rr/5. + 1
3089  elseif(rr .lt. 25.) then
3090  j=4
3091  elseif(rr .lt. 50.) then
3092  j=5
3093  elseif(rr .lt. 150.) then
3094  j=(rr-50.)/50.+6
3095  endif
3096  if(rr .ge. 150.) then
3097  rl=log10(rr)
3098  j=(rl-2.)*4. +1
3099  call kfrges(e2(1, j), 1, 101, de, l, icon)
3100  if(icon .ne. 0) then
3101  fr=0.
3102  else
3103  tmp=0.01/(e2(l+1,j)-e2(l,j)) * (de-e2(l,j)) + (l-1)*0.01
3104  fr=1.-tmp
3105  if(j .eq. 1) then
3106  call kfrges(e1(1,7), 1, 101, de, l, icon)
3107  tmp=0.01/(e1(l+1,7)-e1(l,7)) * (de-e1(l,7)) +
3108  * (l-1)*0.01
3109  fr2=1.-tmp
3110  fr=-(fr2-fr)/13.9* (rr-139.)+ fr
3111  else
3112  call kfrges(e2(1, j-1), 1, 101, de, l, icon)
3113  tmp=0.01/(e2(l+1,j-1)-e2(l,j-1)) * (de-e2(l,j-1))
3114  * + (l-1)*0.01
3115  fr2=1.-tmp
3116  fr= (fr-fr2)/.25 * (rl- (j-1)*.25-2.125) + fr
3117  endif
3118  endif
3119  else
3120  call kfrges(e1(1, j), 1, 101, de, l, icon)
3121  if(icon .ne. 0) then
3122  fr=0.
3123  else
3124  tmp=0.01/(e1(l+1,j)-e1(l,j)) * (de-e1(l,j)) + (l-1)*0.01
3125  fr=1.-tmp
3126  if(j .eq. 2 )then
3127  call kfrges(e1(1,1), 1, 101, de, l, icon)
3128  tmp=0.01/(e1(l+1,1)-e1(l,1)) * (de-e1(l,1)) +
3129  * (l-1)*0.01
3130  fr2=1.-tmp
3131  fr=-(fr2-fr)/5. * (rr-7.5) + fr
3132  elseif(j .eq. 1 )then
3133  call kfrges(e1(1,2), 1, 101, de, l, icon)
3134  tmp=0.01/(e1(l+1,2)-e1(l,2)) * (de-e1(l,2)) +
3135  * (l-1)*0.01
3136  fr2=1.-tmp
3137  fr= (fr2-fr)/5. * (rr-2.5) + fr
3138  elseif(j .eq. 3) then
3139  call kfrges(e1(1,2), 1, 101, de, l, icon)
3140  tmp=0.01/(e1(l+1,2)-e1(l,2)) * (de-e1(l,2)) +
3141  * (l-1)*0.01
3142  fr2=1.-tmp
3143  fr=-(fr2-fr)/5. * (rr-12.5)+ fr
3144  elseif(j .eq. 4) then
3145  call kfrges(e1(1,3), 1, 101, de, l, icon)
3146  tmp=0.01/(e1(l+1,3)-e1(l,3)) * (de-e1(l,3)) +
3147  * (l-1)*0.01
3148  fr2=1.-tmp
3149  fr=-(fr2-fr)/7.5 * (rr-20.)+ fr
3150  elseif(j .eq. 5) then
3151  call kfrges(e1(1,4), 1, 101, de, l, icon)
3152  tmp=0.01/(e1(l+1,4)-e1(l,4)) * (de-e1(l,4)) +
3153  * (l-1)*0.01
3154  fr2=1.-tmp
3155  fr=-(fr2-fr)/17.5* (rr-37.5)+ fr
3156  elseif(j .eq. 6) then
3157  call kfrges(e1(1,5), 1, 101, de, l, icon)
3158  tmp=0.01/(e1(l+1,5)-e1(l,5)) * (de-e1(l,5)) +
3159  * (l-1)*0.01
3160  fr2=1.-tmp
3161  fr=-(fr2-fr)/37.5* (rr-75.)+ fr
3162  elseif(j .eq. 7) then
3163  call kfrges(e1(1,6), 1, 101, de, l, icon)
3164  tmp=0.01/(e1(l+1,6)-e1(l,6)) * (de-e1(l,6)) +
3165  * (l-1)*0.01
3166  fr2=1.-tmp
3167  fr=-(fr2-fr)/50.* (rr-125.)+ fr
3168  endif
3169  endif
3170  endif
r
*Zfirst p fm *Zfirst p Zfirst p Zfirst p *Zfirst p *Zfirst pos xyz r
Definition: ZavoidUnionMap.h:1
j
********************block data cblkHeavy ********************integer j data *HeavyG2symbol *data *HeavyG2code kiron data j
Definition: cblkHeavy.h:36
kfrges
subroutine kfrges(x, intvx, n, c, m, icon)
Definition: genas.f:3434
Here is the call graph for this function:
Here is the caller graph for this function:

◆ kide2()

subroutine kide2 (   de,
  r,
  fr 
)

Definition at line 3173 of file genas.f.

References j, kfrges(), and r.

Referenced by kide().

3173 ! de: input. energy deposit in scintillater. in mev
3174 ! r: input. distance from the core in m
3175 ! fr: output. fraction of particles > de at r.
3176 !
3177  include "Zdeg2"
3178 !
3179 !
3180  if(r .gt. 1780.) then
3181  rr=1333.
3182  else
3183  rr=r
3184  endif
3185  if(rr .lt. 15.) then
3186  j=rr/5. + 1
3187  elseif(rr .lt. 25.) then
3188  j=4
3189  elseif(rr .lt. 50.) then
3190  j=5
3191  elseif(rr .lt. 150.) then
3192  j=(rr-50.)/50.+6
3193  endif
3194  if(rr .ge. 150.) then
3195  rl=log10(rr)
3196  j=(rl-2.)*4. +1
3197  call kfrges(e2(1, j), 1, 101, de, l, icon)
3198  if(icon .ne. 0) then
3199  fr=0.
3200  else
3201  tmp=0.01/(e2(l+1,j)-e2(l,j)) * (de-e2(l,j)) + (l-1)*0.01
3202  fr=1.-tmp
3203  if(j .eq. 1) then
3204  call kfrges(e1(1,7), 1, 101, de, l, icon)
3205  tmp=0.01/(e1(l+1,7)-e1(l,7)) * (de-e1(l,7)) +
3206  * (l-1)*0.01
3207  fr2=1.-tmp
3208  fr=-(fr2-fr)/13.9* (rr-139.)+ fr
3209  else
3210  call kfrges(e2(1, j-1), 1, 101, de, l, icon)
3211  tmp=0.01/(e2(l+1,j-1)-e2(l,j-1)) * (de-e2(l,j-1))
3212  * + (l-1)*0.01
3213  fr2=1.-tmp
3214  fr= (fr-fr2)/.25 * (rl- (j-1)*.25-2.125) + fr
3215  endif
3216  endif
3217  else
3218  call kfrges(e1(1, j), 1, 101, de, l, icon)
3219  if(icon .ne. 0) then
3220  fr=0.
3221  else
3222  tmp=0.01/(e1(l+1,j)-e1(l,j)) * (de-e1(l,j)) + (l-1)*0.01
3223  fr=1.-tmp
3224  if(j .eq. 2 )then
3225  call kfrges(e1(1,1), 1, 101, de, l, icon)
3226  tmp=0.01/(e1(l+1,1)-e1(l,1)) * (de-e1(l,1)) +
3227  * (l-1)*0.01
3228  fr2=1.-tmp
3229  fr=-(fr2-fr)/5. * (rr-7.5) + fr
3230  elseif(j .eq. 1 )then
3231  call kfrges(e1(1,2), 1, 101, de, l, icon)
3232  tmp=0.01/(e1(l+1,2)-e1(l,2)) * (de-e1(l,2)) +
3233  * (l-1)*0.01
3234  fr2=1.-tmp
3235  fr= (fr2-fr)/5. * (rr-2.5) + fr
3236  elseif(j .eq. 3) then
3237  call kfrges(e1(1,2), 1, 101, de, l, icon)
3238  tmp=0.01/(e1(l+1,2)-e1(l,2)) * (de-e1(l,2)) +
3239  * (l-1)*0.01
3240  fr2=1.-tmp
3241  fr=-(fr2-fr)/5. * (rr-12.5)+ fr
3242  elseif(j .eq. 4) then
3243  call kfrges(e1(1,3), 1, 101, de, l, icon)
3244  tmp=0.01/(e1(l+1,3)-e1(l,3)) * (de-e1(l,3)) +
3245  * (l-1)*0.01
3246  fr2=1.-tmp
3247  fr=-(fr2-fr)/7.5 * (rr-20.)+ fr
3248  elseif(j .eq. 5) then
3249  call kfrges(e1(1,4), 1, 101, de, l, icon)
3250  tmp=0.01/(e1(l+1,4)-e1(l,4)) * (de-e1(l,4)) +
3251  * (l-1)*0.01
3252  fr2=1.-tmp
3253  fr=-(fr2-fr)/17.5* (rr-37.5)+ fr
3254  elseif(j .eq. 6) then
3255  call kfrges(e1(1,5), 1, 101, de, l, icon)
3256  tmp=0.01/(e1(l+1,5)-e1(l,5)) * (de-e1(l,5)) +
3257  * (l-1)*0.01
3258  fr2=1.-tmp
3259  fr=-(fr2-fr)/37.5* (rr-75.)+ fr
3260  elseif(j .eq. 7) then
3261  call kfrges(e1(1,6), 1, 101, de, l, icon)
3262  tmp=0.01/(e1(l+1,6)-e1(l,6)) * (de-e1(l,6)) +
3263  * (l-1)*0.01
3264  fr2=1.-tmp
3265  fr=-(fr2-fr)/50.* (rr-125.)+ fr
3266  endif
3267  endif
3268  endif
r
*Zfirst p fm *Zfirst p Zfirst p Zfirst p *Zfirst p *Zfirst pos xyz r
Definition: ZavoidUnionMap.h:1
j
********************block data cblkHeavy ********************integer j data *HeavyG2symbol *data *HeavyG2code kiron data j
Definition: cblkHeavy.h:36
kfrges
subroutine kfrges(x, intvx, n, c, m, icon)
Definition: genas.f:3434
Here is the call graph for this function:
Here is the caller graph for this function:

◆ kide3()

subroutine kide3 (   de,
  r,
  fr 
)

Definition at line 3271 of file genas.f.

References j, kfrges(), and r.

Referenced by kide().

3271 ! de: input. energy deposit in scintillater. in mev
3272 ! r: input. distance from the core in m
3273 ! fr: output. fraction of particles > de at r.
3274 !
3275 ! cos=.7
3276  include "Zdeg3"
3277 !
3278 !
3279  if(r .gt. 1780.) then
3280  rr=1333.
3281  else
3282  rr=r
3283  endif
3284  if(rr .lt. 15.) then
3285  j=rr/5. + 1
3286  elseif(rr .lt. 25.) then
3287  j=4
3288  elseif(rr .lt. 50.) then
3289  j=5
3290  elseif(rr .lt. 150.) then
3291  j=(rr-50.)/50.+6
3292  endif
3293  if(rr .ge. 150.) then
3294  rl=log10(rr)
3295  j=(rl-2.)*4. +1
3296  call kfrges(e2(1, j), 1, 101, de, l, icon)
3297  if(icon .ne. 0) then
3298  fr=0.
3299  else
3300  tmp=0.01/(e2(l+1,j)-e2(l,j)) * (de-e2(l,j)) + (l-1)*0.01
3301  fr=1.-tmp
3302  if(j .eq. 1) then
3303  call kfrges(e1(1,7), 1, 101, de, l, icon)
3304  tmp=0.01/(e1(l+1,7)-e1(l,7)) * (de-e1(l,7)) +
3305  * (l-1)*0.01
3306  fr2=1.-tmp
3307  fr=-(fr2-fr)/13.9* (rr-139.)+ fr
3308  else
3309  call kfrges(e2(1, j-1), 1, 101, de, l, icon)
3310  tmp=0.01/(e2(l+1,j-1)-e2(l,j-1)) * (de-e2(l,j-1))
3311  * + (l-1)*0.01
3312  fr2=1.-tmp
3313  fr= (fr-fr2)/.25 * (rl- (j-1)*.25-2.125) + fr
3314  endif
3315  endif
3316  else
3317  call kfrges(e1(1, j), 1, 101, de, l, icon)
3318  if(icon .ne. 0) then
3319  fr=0.
3320  else
3321  tmp=0.01/(e1(l+1,j)-e1(l,j)) * (de-e1(l,j))
3322  * + (l-1)*0.01
3323  fr=1.-tmp
3324  if(j .eq. 2 )then
3325  call kfrges(e1(1,1), 1, 101, de, l, icon)
3326  tmp=0.01/(e1(l+1,1)-e1(l,1)) * (de-e1(l,1)) +
3327  * (l-1)*0.01
3328  fr2=1.-tmp
3329  fr=-(fr2-fr)/5. * (rr-7.5) + fr
3330  elseif(j .eq. 1 )then
3331  call kfrges(e1(1,2), 1, 101, de, l, icon)
3332  tmp=0.01/(e1(l+1,2)-e1(l,2)) * (de-e1(l,2)) +
3333  * (l-1)*0.01
3334  fr2=1.-tmp
3335  fr= (fr2-fr)/5. * (rr-2.5) + fr
3336  elseif(j .eq. 3) then
3337  call kfrges(e1(1,2), 1, 101, de, l, icon)
3338  tmp=0.01/(e1(l+1,2)-e1(l,2)) * (de-e1(l,2)) +
3339  * (l-1)*0.01
3340  fr2=1.-tmp
3341  fr=-(fr2-fr)/5. * (rr-12.5)+ fr
3342  elseif(j .eq. 4) then
3343  call kfrges(e1(1,3), 1, 101, de, l, icon)
3344  tmp=0.01/(e1(l+1,3)-e1(l,3)) * (de-e1(l,3)) +
3345  * (l-1)*0.01
3346  fr2=1.-tmp
3347  fr=-(fr2-fr)/7.5 * (rr-20.)+ fr
3348  elseif(j .eq. 5) then
3349  call kfrges(e1(1,4), 1, 101, de, l, icon)
3350  tmp=0.01/(e1(l+1,4)-e1(l,4)) * (de-e1(l,4)) +
3351  * (l-1)*0.01
3352  fr2=1.-tmp
3353  fr=-(fr2-fr)/17.5* (rr-37.5)+ fr
3354  elseif(j .eq. 6) then
3355  call kfrges(e1(1,5), 1, 101, de, l, icon)
3356  tmp=0.01/(e1(l+1,5)-e1(l,5)) * (de-e1(l,5)) +
3357  * (l-1)*0.01
3358  fr2=1.-tmp
3359  fr=-(fr2-fr)/37.5* (rr-75.)+ fr
3360  elseif(j .eq. 7) then
3361  call kfrges(e1(1,6), 1, 101, de, l, icon)
3362  tmp=0.01/(e1(l+1,6)-e1(l,6)) * (de-e1(l,6)) +
3363  * (l-1)*0.01
3364  fr2=1.-tmp
3365  fr=-(fr2-fr)/50.* (rr-125.)+ fr
3366  endif
3367  endif
3368  endif
r
*Zfirst p fm *Zfirst p Zfirst p Zfirst p *Zfirst p *Zfirst pos xyz r
Definition: ZavoidUnionMap.h:1
j
********************block data cblkHeavy ********************integer j data *HeavyG2symbol *data *HeavyG2code kiron data j
Definition: cblkHeavy.h:36
kfrges
subroutine kfrges(x, intvx, n, c, m, icon)
Definition: genas.f:3434
Here is the call graph for this function:
Here is the caller graph for this function:

◆ kideb()

subroutine kideb (   e0,
  zob,
  s,
  cosz,
  j1,
  rr,
  de,
  fr 
)

Definition at line 2728 of file genas.f.

References kideb1(), kideb2(), kideb3(), kmolu(), r, stzss(), and z.

Referenced by kdigb(), kdipb(), kfrac(), kudigb(), and kudipb().

2728 ! e0: input. 1ry energy of gamma in tev
2729 ! zob: input. observation depth (g/cm**2) (vetical)
2730 ! s: input. age of the shower
2731 ! cosz: input. cos of the zenith angle of the shower
2732 ! j1: input. 0--> all above parameters are not equal to
2733 ! those in previous call.
2734 ! ^=0-->all above parameters are equal to those
2735 ! in the previous call.
2736 ! de: input. energy deposit in scintillater. in mev
2737 ! rr: input. distance from the core in m
2738 ! fr: output. fraction of particles > de at r.
2739 !
2740  include "Zascns"
2741 !
2742  data ssave/5./
2743  save ssave, um1, um2, rcnv
2744  if(j1 .eq. 0) then
2745 ! new parameters
2746  if(abs(s/ssave-1.) .gt. smarg) then
2747  ssave=s
2748 ! um1=m.u (2 r.l above the observation depht,
2749 ! along the 1ry direction) (in m)
2750  call kmolu(zob, cosz, um1)
2751 ! um2=m.u (same as above) for the dpeth where
2752 ! the standard shower takes the same age (=s) as the
2753 ! currently considered shower.
2754  call stzss(s, z)
2755  call kmolu(z, cosz, um2)
2756  rcnv= sqrt( ssmu * um2)/um1
2757  endif
2758  endif
2759  if(de .gt. 0.) then
2760 ! effective r; ssmu is in Zascns (standard shower m.u)
2761  r=rr* rcnv
2762  if(e0 .lt. .1) then
2763  r=r+10.
2764  endif
2765  if(cosz .gt. .9) then
2766 ! use vertical one
2767  deo=de*cosz
2768  call kideb1(deo, r, fr)
2769  elseif(cosz .gt. .75) then
2770 ! use cos=0.8
2771  deo=de*cosz/0.8
2772  call kideb2(deo, r, fr)
2773  else
2774 ! use cos=0.7
2775  deo=de*cosz/0.7
2776  call kideb3(deo, r, fr)
2777  endif
2778  else
2779  fr=1.
2780  endif
z
nodes z
Definition: cstdatmos0.fNew2.h:93
kideb2
subroutine kideb2(de, r, fr)
Definition: genas.f:2880
r
*Zfirst p fm *Zfirst p Zfirst p Zfirst p *Zfirst p *Zfirst pos xyz r
Definition: ZavoidUnionMap.h:1
kmolu
subroutine kmolu(dep, cosz, rmu)
Definition: genas.f:3583
kideb1
subroutine kideb1(de, r, fr)
Definition: genas.f:2783
kideb3
subroutine kideb3(de, r, fr)
Definition: genas.f:2977
stzss
subroutine stzss(S, Z)
Definition: genas.f:3713
Here is the call graph for this function:
Here is the caller graph for this function:

◆ kideb1()

subroutine kideb1 (   de,
  r,
  fr 
)

Definition at line 2783 of file genas.f.

References j, kfrges(), and r.

Referenced by kideb().

2783 ! de: input. energy deposit in scintillater. in mev
2784 ! r: input. distance from the core in m
2785 ! fr: output. fraction of particles > de at r.
2786 !
2787  include "Zdegb"
2788 !
2789  if(r .gt. 1780.) then
2790  rr=1333.
2791  else
2792  rr=r
2793  endif
2794  if(rr .lt. 15.) then
2795  j=rr/5. + 1
2796  elseif(rr .lt. 25.) then
2797  j=4
2798  elseif(rr .lt. 50.) then
2799  j=5
2800  elseif(rr .lt. 150.) then
2801  j=(rr-50.)/50.+6
2802  endif
2803  if(rr .ge. 150.) then
2804  rl=log10(rr)
2805  j=(rl-2.)*4. +1
2806  call kfrges(e2(1, j), 1, 101, de, l, icon)
2807  if(icon .ne. 0) then
2808  fr=0.
2809  else
2810  tmp=0.01/(e2(l+1,j)-e2(l,j)) * (de-e2(l,j)) + (l-1)*0.01
2811  fr=1.-tmp
2812  if(j .eq. 1) then
2813  call kfrges(e1(1,7), 1, 101, de, l, icon)
2814  tmp=0.01/(e1(l+1,7)-e1(l,7)) * (de-e1(l,7)) +
2815  * (l-1)*0.01
2816  fr2=1.-tmp
2817  fr=-(fr2-fr)/13.9* (rr-139.)+ fr
2818  else
2819  call kfrges(e2(1, j-1), 1, 101, de, l, icon)
2820  tmp=0.01/(e2(l+1,j-1)-e2(l,j-1)) * (de-e2(l,j-1))
2821  * + (l-1)*0.01
2822  fr2=1.-tmp
2823  fr= (fr-fr2)/.25 * (rl- (j-1)*.25-2.125) + fr
2824  endif
2825  endif
2826  else
2827  call kfrges(e1(1, j), 1, 101, de, l, icon)
2828  if(icon .ne. 0) then
2829  fr=0.
2830  else
2831  tmp=0.01/(e1(l+1,j)-e1(l,j)) * (de-e1(l,j)) + (l-1)*0.01
2832  fr=1.-tmp
2833  if(j .eq. 2 )then
2834  call kfrges(e1(1,1), 1, 101, de, l, icon)
2835  tmp=0.01/(e1(l+1,1)-e1(l,1)) * (de-e1(l,1)) +
2836  * (l-1)*0.01
2837  fr2=1.-tmp
2838  fr=-(fr2-fr)/5. * (rr-7.5) + fr
2839  elseif(j .eq. 1 )then
2840  call kfrges(e1(1,2), 1, 101, de, l, icon)
2841  tmp=0.01/(e1(l+1,2)-e1(l,2)) * (de-e1(l,2)) +
2842  * (l-1)*0.01
2843  fr2=1.-tmp
2844  fr= (fr2-fr)/5. * (rr-2.5) + fr
2845  elseif(j .eq. 3) then
2846  call kfrges(e1(1,2), 1, 101, de, l, icon)
2847  tmp=0.01/(e1(l+1,2)-e1(l,2)) * (de-e1(l,2)) +
2848  * (l-1)*0.01
2849  fr2=1.-tmp
2850  fr=-(fr2-fr)/5. * (rr-12.5)+ fr
2851  elseif(j .eq. 4) then
2852  call kfrges(e1(1,3), 1, 101, de, l, icon)
2853  tmp=0.01/(e1(l+1,3)-e1(l,3)) * (de-e1(l,3)) +
2854  * (l-1)*0.01
2855  fr2=1.-tmp
2856  fr=-(fr2-fr)/7.5 * (rr-20.)+ fr
2857  elseif(j .eq. 5) then
2858  call kfrges(e1(1,4), 1, 101, de, l, icon)
2859  tmp=0.01/(e1(l+1,4)-e1(l,4)) * (de-e1(l,4)) +
2860  * (l-1)*0.01
2861  fr2=1.-tmp
2862  fr=-(fr2-fr)/17.5* (rr-37.5)+ fr
2863  elseif(j .eq. 6) then
2864  call kfrges(e1(1,5), 1, 101, de, l, icon)
2865  tmp=0.01/(e1(l+1,5)-e1(l,5)) * (de-e1(l,5)) +
2866  * (l-1)*0.01
2867  fr2=1.-tmp
2868  fr=-(fr2-fr)/37.5* (rr-75.)+ fr
2869  elseif(j .eq. 7) then
2870  call kfrges(e1(1,6), 1, 101, de, l, icon)
2871  tmp=0.01/(e1(l+1,6)-e1(l,6)) * (de-e1(l,6)) +
2872  * (l-1)*0.01
2873  fr2=1.-tmp
2874  fr=-(fr2-fr)/50.* (rr-125.)+ fr
2875  endif
2876  endif
2877  endif
r
*Zfirst p fm *Zfirst p Zfirst p Zfirst p *Zfirst p *Zfirst pos xyz r
Definition: ZavoidUnionMap.h:1
j
********************block data cblkHeavy ********************integer j data *HeavyG2symbol *data *HeavyG2code kiron data j
Definition: cblkHeavy.h:36
kfrges
subroutine kfrges(x, intvx, n, c, m, icon)
Definition: genas.f:3434
Here is the call graph for this function:
Here is the caller graph for this function:

◆ kideb2()

subroutine kideb2 (   de,
  r,
  fr 
)

Definition at line 2880 of file genas.f.

References j, kfrges(), and r.

Referenced by kideb().

2880 ! de: input. energy deposit in scintillater. in mev
2881 ! r: input. distance from the core in m
2882 ! fr: output. fraction of particles > de at r.
2883 !
2884  include "Zdegb2"
2885 !
2886  if(r .gt. 3162.) then
2887  rr=2371.
2888  else
2889  rr=r
2890  endif
2891  if(rr .lt. 15.) then
2892  j=rr/5. + 1
2893  elseif(rr .lt. 25.) then
2894  j=4
2895  elseif(rr .lt. 50.) then
2896  j=5
2897  elseif(rr .lt. 150.) then
2898  j=(rr-50.)/50.+6
2899  endif
2900  if(rr .ge. 150.) then
2901  rl=log10(rr)
2902  j=(rl-2.)*4. +1
2903  call kfrges(e2(1, j), 1, 101, de, l, icon)
2904  if(icon .ne. 0) then
2905  fr=0.
2906  else
2907  tmp=0.01/(e2(l+1,j)-e2(l,j)) * (de-e2(l,j)) + (l-1)*0.01
2908  fr=1.-tmp
2909  if(j .eq. 1) then
2910  call kfrges(e1(1,7), 1, 101, de, l, icon)
2911  tmp=0.01/(e1(l+1,7)-e1(l,7)) * (de-e1(l,7)) +
2912  * (l-1)*0.01
2913  fr2=1.-tmp
2914  fr=-(fr2-fr)/13.9* (rr-139.)+ fr
2915  else
2916  call kfrges(e2(1, j-1), 1, 101, de, l, icon)
2917  tmp=0.01/(e2(l+1,j)-e2(l,j)) * (de-e2(l,j))
2918  * + (l-1)*0.01
2919  fr2=1.-tmp
2920  fr= (fr-fr2)/.25 * (rl- (j-1)*.25-2.125) + fr
2921  endif
2922  endif
2923  else
2924  call kfrges(e1(1, j), 1, 101, de, l, icon)
2925  if(icon .ne. 0) then
2926  fr=0.
2927  else
2928  tmp=0.01/(e1(l+1,j)-e1(l,j)) * (de-e1(l,j)) + (l-1)*0.01
2929  fr=1.-tmp
2930  if(j .eq. 2 )then
2931  call kfrges(e1(1,1), 1, 101, de, l, icon)
2932  tmp=0.01/(e1(l+1,1)-e1(l,1)) * (de-e1(l,1)) +
2933  * (l-1)*0.01
2934  fr2=1.-tmp
2935  fr=-(fr2-fr)/5. * (rr-7.5) + fr
2936  elseif(j .eq. 1 )then
2937  call kfrges(e1(1,2), 1, 101, de, l, icon)
2938  tmp=0.01/(e1(l+1,2)-e1(l,2)) * (de-e1(l,2)) +
2939  * (l-1)*0.01
2940  fr2=1.-tmp
2941  fr= (fr2-fr)/5. * (rr-2.5) + fr
2942  elseif(j .eq. 3) then
2943  call kfrges(e1(1,2), 1, 101, de, l, icon)
2944  tmp=0.01/(e1(l+1,2)-e1(l,2)) * (de-e1(l,2)) +
2945  * (l-1)*0.01
2946  fr2=1.-tmp
2947  fr=-(fr2-fr)/5. * (rr-12.5)+ fr
2948  elseif(j .eq. 4) then
2949  call kfrges(e1(1,3), 1, 101, de, l, icon)
2950  tmp=0.01/(e1(l+1,3)-e1(l,3)) * (de-e1(l,3)) +
2951  * (l-1)*0.01
2952  fr2=1.-tmp
2953  fr=-(fr2-fr)/7.5 * (rr-20.)+ fr
2954  elseif(j .eq. 5) then
2955  call kfrges(e1(1,4), 1, 101, de, l, icon)
2956  tmp=0.01/(e1(l+1,4)-e1(l,4)) * (de-e1(l,4)) +
2957  * (l-1)*0.01
2958  fr2=1.-tmp
2959  fr=-(fr2-fr)/17.5* (rr-37.5)+ fr
2960  elseif(j .eq. 6) then
2961  call kfrges(e1(1,5), 1, 101, de, l, icon)
2962  tmp=0.01/(e1(l+1,5)-e1(l,5)) * (de-e1(l,5)) +
2963  * (l-1)*0.01
2964  fr2=1.-tmp
2965  fr=-(fr2-fr)/37.5* (rr-75.)+ fr
2966  elseif(j .eq. 7) then
2967  call kfrges(e1(1,6), 1, 101, de, l, icon)
2968  tmp=0.01/(e1(l+1,6)-e1(l,6)) * (de-e1(l,6)) +
2969  * (l-1)*0.01
2970  fr2=1.-tmp
2971  fr=-(fr2-fr)/50.* (rr-125.)+ fr
2972  endif
2973  endif
2974  endif
r
*Zfirst p fm *Zfirst p Zfirst p Zfirst p *Zfirst p *Zfirst pos xyz r
Definition: ZavoidUnionMap.h:1
j
********************block data cblkHeavy ********************integer j data *HeavyG2symbol *data *HeavyG2code kiron data j
Definition: cblkHeavy.h:36
kfrges
subroutine kfrges(x, intvx, n, c, m, icon)
Definition: genas.f:3434
Here is the call graph for this function:
Here is the caller graph for this function:

◆ kideb3()

subroutine kideb3 (   de,
  r,
  fr 
)

Definition at line 2977 of file genas.f.

References j, kfrges(), and r.

Referenced by kideb().

2977 ! de: input. energy deposit in scintillater. in mev
2978 ! r: input. distance from the core in m
2979 ! fr: output. fraction of particles > de at r.
2980 !
2981  include "Zdegb3"
2982 !
2983  if(r .gt. 3162.) then
2984  rr=2371.
2985  else
2986  rr=r
2987  endif
2988  if(rr .lt. 15.) then
2989  j=rr/5. + 1
2990  elseif(rr .lt. 25.) then
2991  j=4
2992  elseif(rr .lt. 50.) then
2993  j=5
2994  elseif(rr .lt. 150.) then
2995  j=(rr-50.)/50.+6
2996  endif
2997  if(rr .ge. 150.) then
2998  rl=log10(rr)
2999  j=(rl-2.)*4. +1
3000  call kfrges(e2(1, j), 1, 101, de, l, icon)
3001  if(icon .ne. 0) then
3002  fr=0.
3003  else
3004  tmp=0.01/(e2(l+1,j)-e2(l,j)) * (de-e2(l,j)) + (l-1)*0.01
3005  fr=1.-tmp
3006  if(j .eq. 1) then
3007  call kfrges(e1(1,7), 1, 101, de, l, icon)
3008  tmp=0.01/(e1(l+1,7)-e1(l,7)) * (de-e1(l,7)) +
3009  * (l-1)*0.01
3010  fr2=1.-tmp
3011  fr=-(fr2-fr)/13.9* (rr-139.)+ fr
3012  else
3013  call kfrges(e2(1, j-1), 1, 101, de, l, icon)
3014  tmp=0.01/(e2(l+1,j)-e2(l,j)) * (de-e2(l,j))
3015  * + (l-1)*0.01
3016  fr2=1.-tmp
3017  fr= (fr-fr2)/.25 * (rl- (j-1)*.25-2.125) + fr
3018  endif
3019  endif
3020  else
3021  call kfrges(e1(1, j), 1, 101, de, l, icon)
3022  if(icon .ne. 0) then
3023  fr=0.
3024  else
3025  tmp=0.01/(e1(l+1,j)-e1(l,j)) * (de-e1(l,j)) + (l-1)*0.01
3026  fr=1.-tmp
3027  if(j .eq. 2 )then
3028  call kfrges(e1(1,1), 1, 101, de, l, icon)
3029  tmp=0.01/(e1(l+1,1)-e1(l,1)) * (de-e1(l,1)) +
3030  * (l-1)*0.01
3031  fr2=1.-tmp
3032  fr=-(fr2-fr)/5. * (rr-7.5) + fr
3033  elseif(j .eq. 1 )then
3034  call kfrges(e1(1,2), 1, 101, de, l, icon)
3035  tmp=0.01/(e1(l+1,2)-e1(l,2)) * (de-e1(l,2)) +
3036  * (l-1)*0.01
3037  fr2=1.-tmp
3038  fr= (fr2-fr)/5. * (rr-2.5) + fr
3039  elseif(j .eq. 3) then
3040  call kfrges(e1(1,2), 1, 101, de, l, icon)
3041  tmp=0.01/(e1(l+1,2)-e1(l,2)) * (de-e1(l,2)) +
3042  * (l-1)*0.01
3043  fr2=1.-tmp
3044  fr=-(fr2-fr)/5. * (rr-12.5)+ fr
3045  elseif(j .eq. 4) then
3046  call kfrges(e1(1,3), 1, 101, de, l, icon)
3047  tmp=0.01/(e1(l+1,3)-e1(l,3)) * (de-e1(l,3)) +
3048  * (l-1)*0.01
3049  fr2=1.-tmp
3050  fr=-(fr2-fr)/7.5 * (rr-20.)+ fr
3051  elseif(j .eq. 5) then
3052  call kfrges(e1(1,4), 1, 101, de, l, icon)
3053  tmp=0.01/(e1(l+1,4)-e1(l,4)) * (de-e1(l,4)) +
3054  * (l-1)*0.01
3055  fr2=1.-tmp
3056  fr=-(fr2-fr)/17.5* (rr-37.5)+ fr
3057  elseif(j .eq. 6) then
3058  call kfrges(e1(1,5), 1, 101, de, l, icon)
3059  tmp=0.01/(e1(l+1,5)-e1(l,5)) * (de-e1(l,5)) +
3060  * (l-1)*0.01
3061  fr2=1.-tmp
3062  fr=-(fr2-fr)/37.5* (rr-75.)+ fr
3063  elseif(j .eq. 7) then
3064  call kfrges(e1(1,6), 1, 101, de, l, icon)
3065  tmp=0.01/(e1(l+1,6)-e1(l,6)) * (de-e1(l,6)) +
3066  * (l-1)*0.01
3067  fr2=1.-tmp
3068  fr=-(fr2-fr)/50.* (rr-125.)+ fr
3069  endif
3070  endif
3071  endif
r
*Zfirst p fm *Zfirst p Zfirst p Zfirst p *Zfirst p *Zfirst pos xyz r
Definition: ZavoidUnionMap.h:1
j
********************block data cblkHeavy ********************integer j data *HeavyG2symbol *data *HeavyG2code kiron data j
Definition: cblkHeavy.h:36
kfrges
subroutine kfrges(x, intvx, n, c, m, icon)
Definition: genas.f:3434
Here is the call graph for this function:
Here is the caller graph for this function:

◆ kintp3s()

subroutine kintp3s ( dimension(intv, *)  f,
  intv,
  n,
  x1,
  h,
  x,
  ans 
)

Definition at line 3389 of file genas.f.

References f, h, i, n, p, x, and x1().

3389 !
3390 ! dimension f(intv, n)
3391 ! ( , *) is to avoid possible warning at debug time
3392  dimension f(intv, *)
3393 !
3394  if(n .lt. 3) then
3395  ans=0.
3396  else
3397  i=(x-x1)/h
3398  if(i .lt. 0) then
3399  i=0
3400  elseif(i .gt. 0) then
3401  if(i+3 .gt. n) then
3402  i=n-3
3403  endif
3404  endif
3405  p=(x-x1-h*float(i+1))/h
3406  ta=p-1.
3407  tb=p+1.
3408  ans=0.5*p*(ta*f(1, i+1)+tb*f(1, i+3)) - ta*tb*f(1, i+2)
3409  endif
x1
block data include Zlatfit h c fitting region data x1(1)/0.03/
ans
atmos%rho(atmos%nodes) **exp(-(z-atmos%z(atmos%nodes))/Hinf) elseif(z .lt. atmos%z(1)) then ans=atmos%rho(1) **exp((atmos%z(1) -z)/atmos%H(1)) else call kdwhereis(z, atmos%nodes, atmos%z, 1, i) a=atmos%a(i) if(a .ne. 0.d0) then ans=atmos%rho(i) **(1+a *(z-atmos%z(i))/atmos%H(i)) **(-1.0d0-1.d0/a) else ans=*atmos%rho(i) *exp(-(z-atmos%z(i))/atmos%H(i)) endif endif ! zsave=z ! endif cvh2den=ans end ! ---------------------------------- real *8 function cvh2temp(z) implicit none ! vettical height to temperatur(Kelvin) real *8 z ! input. vertical height in m ! output is temperature of the atmospher in Kelvin real *8 ans integer i if(z .gt. atmos%z(atmos%nodes)) then ans=atmos%T(atmos%nodes) elseif(z .lt. atmos%z(1)) then ans=atmos%T(1)+atmos%b(1) *(z - atmos%z(1)) else call kdwhereis(z, atmos%nodes, atmos%z, 1, i) ans=atmos%T(i)+atmos%b(i) *(z-atmos%z(i)) endif cvh2temp=ans end !--------------------------------------------- real *8 function cthick2h(t) implicit none real *8 t ! input. air thickness in kg/m^2 real *8 logt, ans integer i real *8 dod0, fd, a logt=log(t) if(t .ge. atmos%cumd(1)) then ans=atmos%z(1) - *(logt - atmos%logcumd(1)) *atmos%H(1) elseif(t .le. atmos%cumd(atmos%nodes)) then ans=atmos%z(atmos%nodes) - *Hinf *log(t/atmos%cumd(atmos%nodes)) else call kdwhereis(t, atmos%nodes, atmos%cumd, 1, i) ! i is such that X(i) > x >=x(i+1) ans
Definition: cstdatmos0.fNew2.h:82
i
nodes i
Definition: cstdatmos0.fNew2.h:93
nrl_atmos::h
real(4), dimension(:), allocatable, save h
Definition: cNRLAtmos.f:28
p
********************block data cblkHeavy ********************integer j data *HeavyG2symbol p
Definition: cblkHeavy.h:7
n
integer n
Definition: Zcinippxc.h:1
x
! structure defining a particle at production ! Basic idea of what is to be contained in ! the particle structue is that dynamical ones should be included those derivable from the particle code ! is not included ******************************************************type fmom momentum sequence union map real e endmap map real * x
Definition: Zptcl.h:21
f
dE dx *! Nuc Int sampling table f
Definition: cblkMuInt.h:130
Here is the call graph for this function:

◆ klee()

subroutine klee (   s,
  r,
  rho 
)

kklibg >>>>>>>>>>>>>>>>>>>>>>>>>>>>

Definition at line 3552 of file genas.f.

References parameter(), pi, and r.

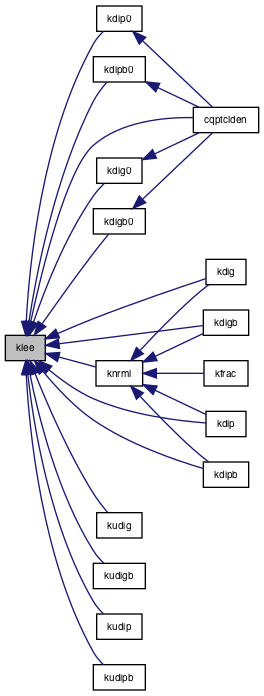
Referenced by cqptclden(), kdig(), kdig0(), kdigb(), kdigb0(), kdip(), kdip0(), kdipb(), kdipb0(), knrml(), kudig(), kudigb(), kudip(), and kudipb().

3552 ! normalized electron lateral distribution for electron
3553 ! primary in the atmsopere.
3554 ! normalization is within 3 % accuracy.
3555 ! s: input. age as determined by 1 dimensional cascade
3556 ! .2 < s < 1.9
3557 ! r: input. distance from the core in moliere unit (
3558 ! m.u should be 2 r.l above
3559 ! the depth ).
3560 ! r>5.e-5
3561 ! rho: output. electron density. integral of 2pi*r* rho(r) dr from
3562 ! 5.e-5 to inf = 1.
3563 !
3564  parameter(p2=.15, p3=.6, pi=3.1415, tpi=2*pi)
3565 !
3566  p1=10.**( (((-0.75222*s+4.4412)*s-10.447)*s +11.531)*s
3567  * -3.8637 )
3568  p4= (.49803*s-2.4992)*s+1.8372
3569  p5=2.4235 - 0.37908*s
3570  if(r .gt. 0.) then
3571  rho= p1 * r**(-p4) * (1.+ r/p2)**(-p3*log10(r)-p5)
3572  * /tpi/r
3573  else
3574  rho=0.
3575  endif
parameter
integer npitbl real *nx parameter(n=101, npitbl=46, nx=n-1) real *8 uconst
r
*Zfirst p fm *Zfirst p Zfirst p Zfirst p *Zfirst p *Zfirst pos xyz r
Definition: ZavoidUnionMap.h:1
pi
! constants thru Cosmos real * pi
Definition: Zglobalc.h:2
Here is the call graph for this function:
Here is the caller graph for this function:

◆ kmolu()

subroutine kmolu (   dep,
  cosz,
  rmu 
)

Definition at line 3583 of file genas.f.

References cgetmoliereu().

Referenced by kide(), kideb(), knrml(), and knrml2().

3583  real*8 ddep ! in kg/m2
3584  real*8 dcosz
3585  real*8 dmu
3586  ddep = dep * 10.
3587  dcosz = cosz
3588  call cgetmoliereu(ddep, dcosz, dmu)
3589  rmu = dmu
cgetmoliereu
subroutine cgetmoliereu(dep, cosz, rmu)
Definition: cgetMoliereU.f:11
Here is the call graph for this function:
Here is the caller graph for this function:

◆ knrml()

subroutine knrml (   e0,
  zob,
  cosz,
  s,
  de,
external  kcfx,
external  kidx,
  sum 
)

Definition at line 3603 of file genas.f.

References e, i, klee(), and kmolu().

Referenced by kdig(), kdigb(), kdip(), kdipb(), and kfrac().

3603 !
3604 ! kcfx: subroutine name.
3605 ! kcfg for kdig (lateral for gamma with fe.1sc3.5)
3606 ! kcfp for kdip (// proton //)
3607 ! kcfgb for kdigb (// for gamma with pb.5fe.1sc3.5)
3608 ! kcfpb for kdipb (// for proton with pb.5fe.1sc3.5)
3609 ! kidx: subroutine name
3610 ! kide for kdig, kdip
3611 ! kideb for kdigb, kdipb
3612 
3613  external kcfx, kidx
3614 
3615  sum=0.
3616  sumuni=0.
3617  call kmolu(zob, cosz, rmu)
3618  if(s .gt. .65) then
3619  r2=1.e-4
3620  dr=.1
3621  imx= 57
3622  jmodx=2
3623  else
3624  r2=3.e-5
3625  dr=.05
3626  imx=100
3627  jmodx=4
3628  endif
3629  dr10=10.**dr
3630  do 100 i=1, imx
3631  r1=r2
3632  r2=r1*dr10
3633  rr=(r1+r2)/2
3634 ! get ne density
3635  call klee(s,rr, rhone)
3636 ! get correction factor rho'/rho
3637  call kcfx(e0, cosz, s, rr, cf)
3638 ! get fraction of particles at rr with >de.
3639 ! r should be in m
3640  if(de .eq. 0.) then
3641  fr=1.
3642  else
3643 ! fr changes slowly with r.
3644  if(mod(i-1,jmodx) .eq. 0) then
3645  call kidx(e0, zob, s, cosz, 0, rr*rmu, de, fr)
3646  endif
3647  endif
3648  tmp=rhone*cf
3649  sumuni=sumuni+ tmp*(r2-r1)*(r1+r2)
3650  rhou=tmp*fr
3651  sum=sum + rhou*(r2-r1)*(r1+r2)
3652  100 continue
3653 ! sumuni=sumuni*3.1415
3654 ! sumuni should be 1. but not, so renormalize
3655 ! sum=sum*3.1415/sumuni
3656  sum=sum/sumuni
e
dE dx *! Nuc Int sampling table e
Definition: cblkMuInt.h:130
i
nodes i
Definition: cstdatmos0.fNew2.h:93
kmolu
subroutine kmolu(dep, cosz, rmu)
Definition: genas.f:3583
klee
subroutine klee(s, r, rho)
kklibg >>>>>>>>>>>>>>>>>>>>>>>>>>>>
Definition: genas.f:3552
Here is the call graph for this function:
Here is the caller graph for this function:

◆ knrml2()

subroutine knrml2 (   e0,
  zob,
  cosz,
  s,
  discle,
external  kcfx,
external  kidx,
  sum 
)

Definition at line 3660 of file genas.f.

References e, i, and kmolu().

3660 !
3661 ! rho(r)*<de> 2pir dr is integrated to give sum,
3662 ! where rho(r) is the density of ptcls which give rise
3663 ! to energy deposit in scinti
3664 ! kcfx: subroutine name.
3665 ! kade for lateral with fe.1sc3.5 (gamma, proton)
3666 ! kadeb for lateral with pb.5fe.1sc3.5(// )
3667 ! kidx: subroutine name
3668 ! kdig for lateral by gamma with fe.1sc3.5
3669 ! kdigb for // pb.5fe.1sc3.5
3670 ! kdip for lateral by proton with fe.1sc3.5
3671 ! kdipb // pb.5fe.1sc3.5
3672 
3673  external kcfx, kidx
3674 
3675  sum=0.
3676  call kmolu(zob, cosz, rmu)
3677  if(s .gt. .65) then
3678  r2=1.e-4
3679  dr=.1
3680  imx= 57
3681  jmodx=2
3682  else
3683  r2=3.e-5
3684  dr=.05
3685  imx=100
3686  jmodx=4
3687  endif
3688  dr10=10.**dr
3689  do 100 i=1, imx
3690  r1=r2
3691  r2=r1*dr10
3692  rr=(r1+r2)/2
3693 ! get ptcl density
3694  call kidx(e0, zob, cosz, s, discle, 1, rr, rho)
3695 ! get average <de>
3696  call kcfx(e0, zob, s, cosz, rr*rmu, avde)
3697  rhou=rho*avde
3698  sum=sum + rhou*(r2-r1)*(r1+r2)
3699  100 continue
3700  sum=sum*3.1415
e
dE dx *! Nuc Int sampling table e
Definition: cblkMuInt.h:130
i
nodes i
Definition: cstdatmos0.fNew2.h:93
kmolu
subroutine kmolu(dep, cosz, rmu)
Definition: genas.f:3583
Here is the call graph for this function:

◆ kudig()

subroutine kudig (   e0,
  zob,
  cosz,
  s,
  de,
  j1,
  r,
  rho 
)

Definition at line 1675 of file genas.f.

References kcfg(), kide(), klee(), and r.

1675 !
1676 ! get density at r for electron
1677  call klee(s, r, rhone)
1678 ! get correction factor due to obseravtion conditions
1679 ! (cascade in detectors).
1680  call kcfg(e0, cosz, s, r, cf)
1681 ! get prob. of energy loss > de
1682  call kide(e0, zob, s, cosz, j1, r, de, fr)
1683  rho=rhone*cf*fr
kide
subroutine kide(e0, zob, s, cosz, j1, rr, de, fr)
Definition: genas.f:2665
r
*Zfirst p fm *Zfirst p Zfirst p Zfirst p *Zfirst p *Zfirst pos xyz r
Definition: ZavoidUnionMap.h:1
klee
subroutine klee(s, r, rho)
kklibg >>>>>>>>>>>>>>>>>>>>>>>>>>>>
Definition: genas.f:3552
kcfg
subroutine kcfg(e0, cosz, s, r, cf)
Definition: genas.f:1765
Here is the call graph for this function:

◆ kudigb()

subroutine kudigb (   e0,
  zob,
  cosz,
  s,
  de,
  j1,
  r,
  rho 
)

Definition at line 1723 of file genas.f.

References kcfgb(), kideb(), klee(), and r.

1723 !
1724  call klee(s, r, rhone)
1725  call kcfgb(e0, cosz, s, r, cf)
1726  call kideb(e0, zob, s, cosz, j1, r, de, fr)
1727  rho=rhone*cf*fr
r
*Zfirst p fm *Zfirst p Zfirst p Zfirst p *Zfirst p *Zfirst pos xyz r
Definition: ZavoidUnionMap.h:1
klee
subroutine klee(s, r, rho)
kklibg >>>>>>>>>>>>>>>>>>>>>>>>>>>>
Definition: genas.f:3552
kideb
subroutine kideb(e0, zob, s, cosz, j1, rr, de, fr)
Definition: genas.f:2728
kcfgb
subroutine kcfgb(e0, cosz, s, r, cf)
Definition: genas.f:1927
Here is the call graph for this function:

◆ kudip()

subroutine kudip (   e0,
  zob,
  cosz,
  s,
  de,
  j1,
  r,
  rho 
)

Definition at line 1687 of file genas.f.

References kcfp(), kide(), klee(), and r.

1687  call klee(s, r, rhone)
1688  call kcfp(e0, cosz, s, r, cf)
1689  call kide(e0, zob, s, cosz, j1, r, de, fr)
1690  rho=rhone*cf*fr
kide
subroutine kide(e0, zob, s, cosz, j1, rr, de, fr)
Definition: genas.f:2665
r
*Zfirst p fm *Zfirst p Zfirst p Zfirst p *Zfirst p *Zfirst pos xyz r
Definition: ZavoidUnionMap.h:1
klee
subroutine klee(s, r, rho)
kklibg >>>>>>>>>>>>>>>>>>>>>>>>>>>>
Definition: genas.f:3552
kcfp
subroutine kcfp(e0, cosz, s, r, cf)
Definition: genas.f:2111
Here is the call graph for this function:

◆ kudipb()

subroutine kudipb (   e0,
  zob,
  cosz,
  s,
  de,
  j1,
  r,
  rho 
)

Definition at line 1731 of file genas.f.

References kcfpb(), kideb(), klee(), and r.

1731  call klee(s, r, rhone)
1732  call kcfpb(e0, cosz, s, r, cf)
1733  call kideb(e0, zob, s, cosz, j1, r, de, fr)
1734  rho=rhone*cf*fr
r
*Zfirst p fm *Zfirst p Zfirst p Zfirst p *Zfirst p *Zfirst pos xyz r
Definition: ZavoidUnionMap.h:1
klee
subroutine klee(s, r, rho)
kklibg >>>>>>>>>>>>>>>>>>>>>>>>>>>>
Definition: genas.f:3552
kideb
subroutine kideb(e0, zob, s, cosz, j1, rr, de, fr)
Definition: genas.f:2728
kcfpb
subroutine kcfpb(e0, cosz, s, r, cf)
Definition: genas.f:2280
Here is the call graph for this function:

◆ rndcsng()

subroutine rndcsng ( real  u)

Definition at line 33 of file genas.f.

References i, and rndc().

Referenced by kgausss().

33  real*8 u8
34  real u
35  call rndc(u8)
36  u = u8
rndc
subroutine rndc(u)
Definition: rnd.f:91
Here is the call graph for this function:
Here is the caller graph for this function:

◆ stndg()

subroutine stndg (   ELG,
  S,
  Z 
)

Definition at line 3730 of file genas.f.

References z.

Referenced by stzss().

3730 ! S(AGE) TO NORMALIZED DEPTH (COG NORMALZIED)
3731 ! ELG: INPUT. LOG10(EG/TEV)
3732 ! S: INPUT. AGE (.4 TO 1.7)
3733 ! Z: OUTPUT. NORMALZIED DEPTH (COG SUBTRACTED ; G/CM**2)
3734 !
3735  IF(s .LT. 0.9) THEN
3736  a1=-81.
3737  b1=72.
3738  c1=0.
3739  a2=-618.
3740  b2=588.5
3741  c2=0.
3742  ELSE
3743 ! A2=-355.46
3744 ! B2=94.706
3745 ! C2=216.07
3746 ! CORRECTED BY SMALL AIR SHOWER BY DIRECT SIM.
3747  a2=-214.5
3748  b2=-191.1
3749  c2=355.6
3750 ! IF(S .LT. 1.1) THEN
3751 ! CORRECTED BY SMALL AIR SHOWER BY DIRECT SIM.
3752  IF(s .LT. 1.3) THEN
3753 ! A1=-150.3
3754 ! B1=150.3
3755  a1=-156.5
3756  b1=156.5
3757  c1=0.
3758  ELSE
3759 ! A1=70.52
3760 ! B1=-229.3
3761 ! C1=162.5
3762 ! CORRECTED BY SMALL AIR SHOWER BY DIRECT SIM.
3763  a1=-219.5
3764  b1=205.0
3765  c1=0.
3766  ENDIF
3767  ENDIF
3768  z=(( c1*s + b1)*s + a1 )*elg + (c2*s+b2)*s+ a2
z
nodes z
Definition: cstdatmos0.fNew2.h:93
Here is the caller graph for this function:

◆ stzss()

subroutine stzss (   S,
  Z 
)

Definition at line 3713 of file genas.f.

References cogg0(), stndg(), and z.

Referenced by kide(), and kideb().

3713 !
3714 ! LOG10(150 (TEV))
3715  DATA elgs/2.175/
3716 !
3717 ! GET COG NORMALIZED DETPH (STANDARD IS ELECTRON OF 100 TEV)
3718 ! WITH Z0=50 G/CM**2.(S=1.075) WE MAY USE GAMMA ROUTINE
3719 ! WITH 150 TEV. (S=1.075===>Z=600)
3720  CALL stndg(elgs, s, z)
3721 ! GET <COG> DEPTH (EXCLUDE 1ST POINT)
3722  CALL cogg0(elgs, cog)
3723 ! ADD 50 G/CM**2
3724  z=z + cog + 50.
3725  IF(z .LE. 0.) THEN
3726  z=5.
3727  ENDIF
z
nodes z
Definition: cstdatmos0.fNew2.h:93
stndg
subroutine stndg(ELG, S, Z)
Definition: genas.f:3730
cogg0
subroutine cogg0(EL, COG)
Definition: genas.f:3771
Here is the call graph for this function:
Here is the caller graph for this function: