Go to the source code of this file.
Functions/Subroutines | |
| subroutine | kcelei (tlat, tlon, dtgmt, height) |
| subroutine | kgcrc (fai, al, h, u, v, w) |
| subroutine | ksidet (year, month, day, time, st) |
| subroutine | kmjd (year, month, day, time, mjd) |
| subroutine | ksided (time, st0, st) |
| subroutine | kside0 (ed, st0) |
| subroutine | ktu (iyear, month, day, ed) |
| subroutine | khtoe (st, hx, hy, hz, ex, ey, ez) |
| subroutine | ketoh (st, ex, ey, ez, hx, hy, hz) |
| subroutine | ketod (delta, alfa, ex, ey, ez) |
| subroutine | kdtoe (ex, ey, ez, delta, alfa) |
| subroutine | kdtoh (hx, hy, hz, teta, fai) |
| subroutine | kadthi (astox) |
| subroutine | kadth (ax, ay, az, hx, hy, hz) |
| subroutine | khtad (hx, hy, hz, ax, ay, az) |
| subroutine | kdhtoh (del, h, w1, w2, w3) |
| subroutine | kdztoh (del, w3, h, icon) |
| subroutine | kdzth2 (del, w3, h, icon) |
| subroutine | keqtog (dec, ra, glat, glon) |
| subroutine | kgtoeq (glat, glon, dec, ra) |
| subroutine | kgdted (gx, gy, gz, ex, ey, ez) |
| subroutine | kmjdym (mjd, y, m, d, time) |
| subroutine | kdcmjd (mjd, iy, im, id, ihr, imn, sec) |
| subroutine | kmjdst (mjd, st) |
| subroutine | kmjdtj (mjd, jd) |
| subroutine | kjtmjd (jd, mjd) |
| subroutine | kpmtrx (mjd, pij) |
| subroutine | kmtoj2 (mjd, t) |
| subroutine | kj2tox (pij, ex2, ey2, ez2, ex, ey, ez) |
| subroutine | kxtoj2 (pij, ex, ey, ez, ex2, ey2, ez2) |
| subroutine | kmoon (mjd, elat, elon, rmoon) |
| real *8 function | ksind (x) |
| real *8 function | kcosd (x) |
| subroutine | kctoq (mjd, cx, cy, cz, ex, ey, ez) |
| subroutine | kqtoc (mjd, ex, ey, ez, cx, cy, cz) |
| subroutine | kmobec (mjd, cose, sine) |
| subroutine | ksuneq (mjd, ex, ey, ez) |
| subroutine | ksun (mjd, slon, rsun) |
| subroutine | kadbp (nftch, dx, dy, dz, dt, wt, u, v, w, tz, icon) |
| subroutine | knormv (a1, b1, c1, fn1) |
| subroutine | kvtoa (vx, vy, vz, teta, fai) |
| subroutine | kdtoa (vx, vy, vz, teta, fai) |
| subroutine | kdifva (a1, a2, b1, b2, c1, c2, difax, |
| subroutine | komeg0 (odec, ora) |
| subroutine | koangl (odec, ora, dec, ra, teta) |
| subroutine | kgcttc (mjd, ex, ey, ez, rs, tex, tey, tez) |
| subroutine | kmoont (mjd, ex, ey, ez) |
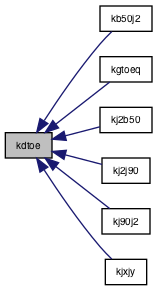
| subroutine | kb50j2 (dec, ra, dec2, ra2) |
| subroutine | kj2b50 (dec2, ra2, dec, ra) |
| subroutine | kj90j2 (dec, ra, dec2, ra2) |
| subroutine | kj2j90 (dec2, ra2, dec, ra) |
| subroutine | kjxjy (mjd1, mjd2, dec1, ra1, dec2, ra2) |
Function/Subroutine Documentation
◆ kadbp()
| subroutine kadbp | ( | nftch, | |
| dimension(nftch) | dx, | ||
| dimension(nftch) | dy, | ||
| dimension(nftch) | dz, | ||
| dimension(nftch) | dt, | ||
| dimension(nftch) | wt, | ||
| u, | |||
| v, | |||
| w, | |||
| tz, | |||
| icon | |||
| ) |
Definition at line 1251 of file kceles.f.
References a, d, d0, dx, h, i, o, p, r, and z.
◆ kadth()
| subroutine kadth | ( | ax, | |
| ay, | |||
| az, | |||
| hx, | |||
| hy, | |||
| hz | |||
| ) |
◆ kadthi()
| subroutine kadthi | ( | astox | ) |
Definition at line 378 of file kceles.f.
References a, cos, cossx, h, o, sinsx, and z.
Referenced by cinitobs().
◆ kb50j2()
| subroutine kb50j2 | ( | dec, | |
| ra, | |||
| dec2, | |||
| ra2 | |||
| ) |
◆ kcelei()
| subroutine kcelei | ( | tlat, | |
| tlon, | |||
| dtgmt, | |||
| height | |||
| ) |
Definition at line 125 of file kceles.f.
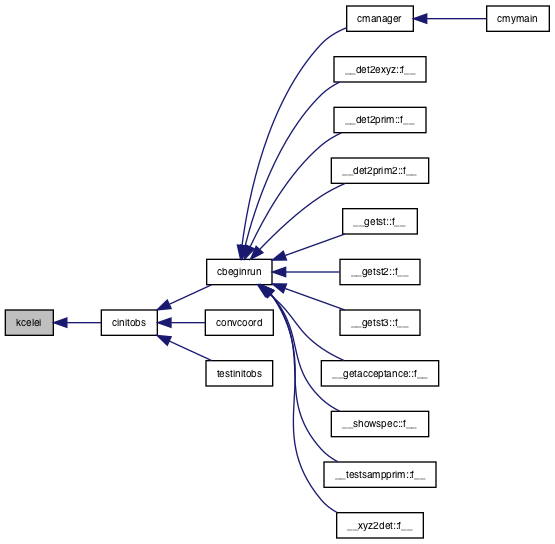
References a, cos, coslat, dtgmts, h, heighs, height, kgcrc(), o, sinlat, tlats, tlons, ug, vg, and z.
Referenced by cinitobs().

◆ kcosd()
| real*8 function kcosd | ( | x | ) |
Definition at line 1091 of file kceles.f.
References a, cos, h, o, x, and z.
◆ kctoq()
| subroutine kctoq | ( | real*8 | mjd, |
| cx, | |||
| cy, | |||
| cz, | |||
| ex, | |||
| ey, | |||
| ez | |||
| ) |
◆ kdcmjd()
| subroutine kdcmjd | ( | real*8 | mjd, |
| iy, | |||
| im, | |||
| id, | |||
| ihr, | |||
| imn, | |||
| sec | |||
| ) |
◆ kdhtoh()
| subroutine kdhtoh | ( | del, | |
| h, | |||
| w1, | |||
| w2, | |||
| w3 | |||
| ) |
Definition at line 408 of file kceles.f.
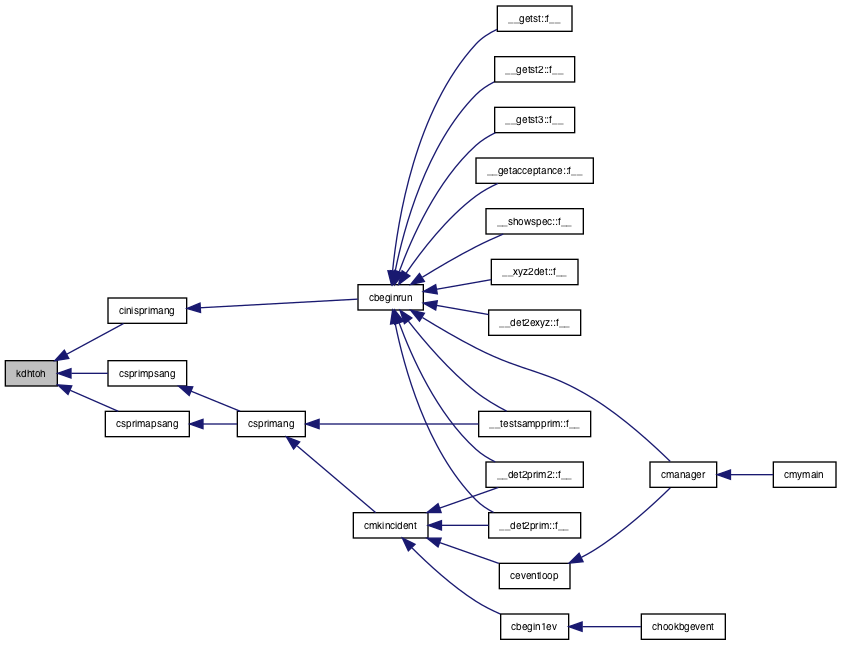
References a, cos, coslat, d0, h, o, sinlat, tofai, and z.
Referenced by cinisprimang(), csprimapsang(), and csprimpsang().
◆ kdifva()
| subroutine kdifva | ( | a1, | |
| a2, | |||
| b1, | |||
| b2, | |||
| c1, | |||
| c2, | |||
| difax | |||
| ) |
◆ kdtoa()
| subroutine kdtoa | ( | vx, | |
| vy, | |||
| vz, | |||
| teta, | |||
| fai | |||
| ) |
◆ kdtoe()
| subroutine kdtoe | ( | ex, | |
| ey, | |||
| ez, | |||
| delta, | |||
| alfa | |||
| ) |
Definition at line 354 of file kceles.f.
References a, d0, f, h, kdtoa(), o, t, and z.
Referenced by kb50j2(), kgtoeq(), kj2b50(), kj2j90(), kj90j2(), and kjxjy().

◆ kdtoh()
| subroutine kdtoh | ( | hx, | |
| hy, | |||
| hz, | |||
| teta, | |||
| fai | |||
| ) |
◆ kdzth2()
| subroutine kdzth2 | ( | del, | |
| w3, | |||
| h, | |||
| icon | |||
| ) |
Definition at line 488 of file kceles.f.
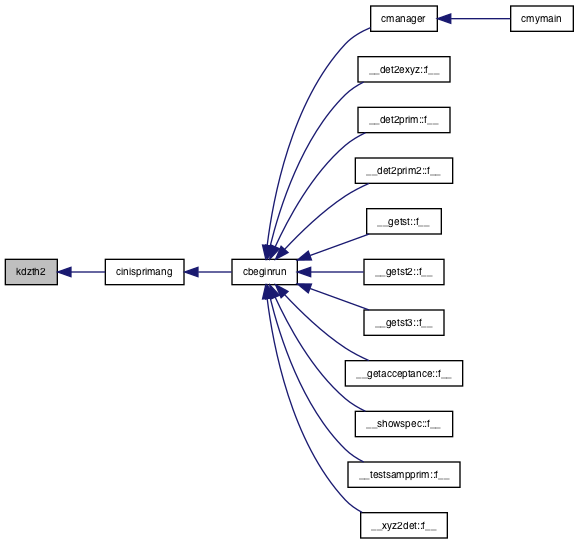
References a, cos, coslat, d, d0, h, o, sinlat, toh, and z.
Referenced by cinisprimang().
◆ kdztoh()
| subroutine kdztoh | ( | del, | |
| w3, | |||
| h, | |||
| icon | |||
| ) |
Definition at line 435 of file kceles.f.
References a, cos, coslat, d, d0, h, o, sinlat, toh, and z.
◆ keqtog()
| subroutine keqtog | ( | dec, | |
| ra, | |||
| glat, | |||
| glon | |||
| ) |
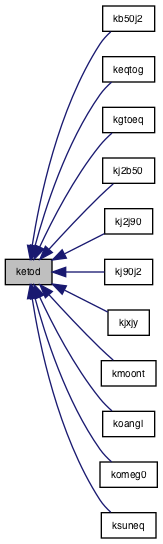
◆ ketod()
| subroutine ketod | ( | delta, | |
| alfa, | |||
| ex, | |||
| ey, | |||
| ez | |||
| ) |
Definition at line 330 of file kceles.f.
References a, cos, h, o, and z.
Referenced by kb50j2(), keqtog(), kgtoeq(), kj2b50(), kj2j90(), kj90j2(), kjxjy(), kmoont(), koangl(), komeg0(), and ksuneq().
◆ ketoh()
| subroutine ketoh | ( | st, | |
| ex, | |||
| ey, | |||
| ez, | |||
| hx, | |||
| hy, | |||
| hz | |||
| ) |
Definition at line 321 of file kceles.f.
References a, cos, coslat, h, o, sinlat, and z.
◆ kgcrc()
| subroutine kgcrc | ( | fai, | |
| al, | |||
| h, | |||
| u, | |||
| v, | |||
| w | |||
| ) |
◆ kgcttc()
| subroutine kgcttc | ( | real*8 | mjd, |
| ex, | |||
| ey, | |||
| ez, | |||
| rs, | |||
| tex, | |||
| tey, | |||
| tez | |||
| ) |
◆ kgdted()
| subroutine kgdted | ( | gx, | |
| gy, | |||
| gz, | |||
| ex, | |||
| ey, | |||
| ez | |||
| ) |
Definition at line 560 of file kceles.f.
References a, cos, d0, f, false, h, o, parameter(), t, and z.
Referenced by kgtoeq().

◆ kgtoeq()
| subroutine kgtoeq | ( | glat, | |
| glon, | |||
| dec, | |||
| ra | |||
| ) |
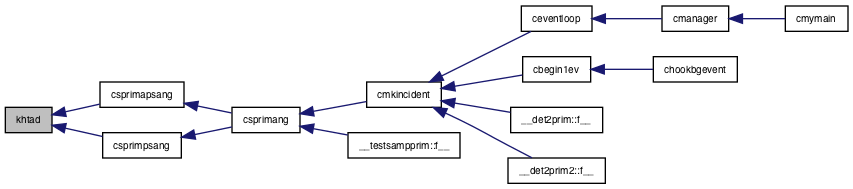
◆ khtad()
| subroutine khtad | ( | hx, | |
| hy, | |||
| hz, | |||
| ax, | |||
| ay, | |||
| az | |||
| ) |
Definition at line 392 of file kceles.f.
References a, cossx, h, o, sinsx, and z.
Referenced by csprimapsang(), and csprimpsang().
◆ khtoe()
| subroutine khtoe | ( | st, | |
| hx, | |||
| hy, | |||
| hz, | |||
| ex, | |||
| ey, | |||
| ez | |||
| ) |
Definition at line 312 of file kceles.f.
References a, cos, coslat, h, o, sinlat, and z.
◆ kj2b50()
| subroutine kj2b50 | ( | dec2, | |
| ra2, | |||
| dec, | |||
| ra | |||
| ) |
◆ kj2j90()
| subroutine kj2j90 | ( | dec2, | |
| ra2, | |||
| dec, | |||
| ra | |||
| ) |
◆ kj2tox()
| subroutine kj2tox | ( | dimension(3,3) | pij, |
| ex2, | |||
| ey2, | |||
| ez2, | |||
| ex, | |||
| ey, | |||
| ez | |||
| ) |
◆ kj90j2()
| subroutine kj90j2 | ( | dec, | |
| ra, | |||
| dec2, | |||
| ra2 | |||
| ) |
◆ kjtmjd()
◆ kjxjy()
◆ kmjd()
◆ kmjdst()
| subroutine kmjdst | ( | real*8 | mjd, |
| st | |||
| ) |
Definition at line 750 of file kceles.f.
References a, d0, h, kmtoj2(), o, parameter(), t, tlons, and z.
Referenced by kgcttc().

◆ kmjdtj()
◆ kmjdym()
Definition at line 641 of file kceles.f.
References a, d0, h, o, time(), and z.
◆ kmobec()
| subroutine kmobec | ( | real*8 | mjd, |
| cose, | |||
| sine | |||
| ) |
Definition at line 1140 of file kceles.f.
References a, cos, d0, h, kmtoj2(), o, t, and z.
Referenced by kctoq(), and kqtoc().

◆ kmoon()
| subroutine kmoon | ( | real*8 | mjd, |
| elat, | |||
| elon, | |||
| rmoon | |||
| ) |
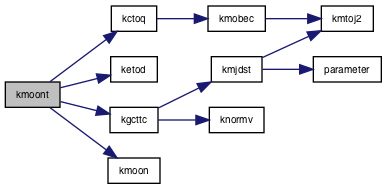
◆ kmoont()
| subroutine kmoont | ( | real*8 | mjd, |
| ex, | |||
| ey, | |||
| ez | |||
| ) |
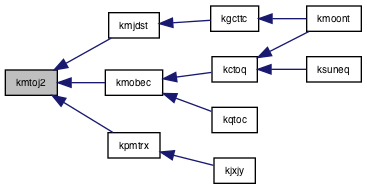
◆ kmtoj2()
◆ knormv()
◆ koangl()
| subroutine koangl | ( | odec, | |
| ora, | |||
| dec, | |||
| ra, | |||
| teta | |||
| ) |
◆ komeg0()
| subroutine komeg0 | ( | odec, | |
| ora | |||
| ) |
Definition at line 1399 of file kceles.f.
References a, d0, h, ketod(), komega, o, parameter(), pi, and z.
◆ kpmtrx()
| subroutine kpmtrx | ( | real*8 | mjd, |
| dimension(3,3) | pij | ||
| ) |
Definition at line 841 of file kceles.f.
References a, cos, d0, h, kmtoj2(), o, parameter(), pi, t, and z.
Referenced by kjxjy().

◆ kqtoc()
| subroutine kqtoc | ( | real*8 | mjd, |
| ex, | |||
| ey, | |||
| ez, | |||
| cx, | |||
| cy, | |||
| cz | |||
| ) |
◆ kside0()
| subroutine kside0 | ( | ed, | |
| st0 | |||
| ) |
Definition at line 263 of file kceles.f.
References a, d0, h, o, parameter(), and z.
Referenced by ksidet().

◆ ksided()
| subroutine ksided | ( | time, | |
| st0, | |||
| st | |||
| ) |
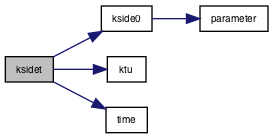
◆ ksidet()
◆ ksind()
| real*8 function ksind | ( | x | ) |
Definition at line 1085 of file kceles.f.
◆ ksun()
| subroutine ksun | ( | real*8 | mjd, |
| slon, | |||
| rsun | |||
| ) |
◆ ksuneq()
| subroutine ksuneq | ( | real*8 | mjd, |
| ex, | |||
| ey, | |||
| ez | |||
| ) |
◆ ktu()
◆ kvtoa()
| subroutine kvtoa | ( | vx, | |
| vy, | |||
| vz, | |||
| teta, | |||
| fai | |||
| ) |