COSMOS v7.655  COSMOSv7655
(AirShowerMC)
Functions/Subroutines
ktrpzIntT2.f File Reference

Go to the source code of this file.

Functions/Subroutines

subroutine ktrpzintt2 (t, intv, n, xt, intvx, a, b, ans)
 

Function/Subroutine Documentation

◆ ktrpzintt2()

subroutine ktrpzintt2 ( real*8, dimension(intv, n)  t,
integer  intv,
integer  n,
real*8, dimension(intvx, n)  xt,
integer  intvx,
real*8  a,
real*8  b,
real*8  ans 
)

Definition at line 5 of file ktrpzIntT2.f.

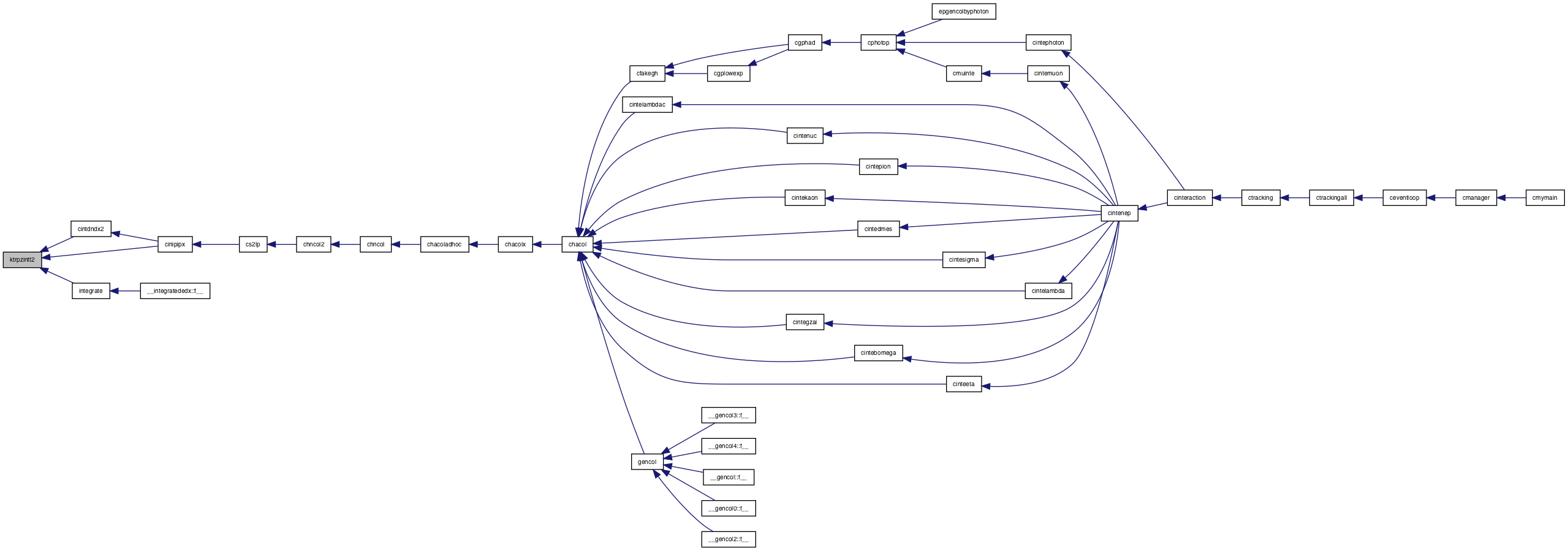
Referenced by cinipipx(), cintdndx2(), and integrate().

5  implicit none
6  integer intv ! input. see below
7  integer n ! input. number of data values
8  real*8 t(intv, n) ! input. t(1, 1), t(1, 2), .. t(1, n) are used.
9  ! function values at xt(1,1), xt(1,2), ..
10  integer intvx ! see below
11  real*8 xt(intvx, n) ! input. must be xt(1,i) < xt(1,i+1)
12  real*8 a ! input. lower value of the integral region.
13  real*8 b ! input. upper value of the integral region. a<= b.
14 ! Note: table values outside of the given xt are assumed to be 0.
15  real*8 ans ! output. integral value
16 
17  integer i, i1, i2
18  real*8 aa, bb, fa, fb
19 
20 
21 
22  ans = 0.
23  aa = max(a, xt(1, 1))
24  bb = min(b, xt(1, n))
25  do i =1, n
26  if(aa .le. xt(1,i)) goto 10
27  enddo
28 ! never come here
29 
30  10 continue
31  i1 = i
32 
33  do i = n, 1, -1
34  if(bb .ge. xt(1,i)) goto 20
35  enddo
36 ! never come here
37 
38  20 continue
39  i2 = i
40 !
41  if(i1 .ne. 1) then
42  fa =
43  * (t(1,i1)- t(1,i1-1))/ (xt(1,i1) - xt(1,i1-1)) *
44  * (aa - xt(1,i1-1)) + t(1,i1-1)
45  ans = ans + (xt(1,i1)- aa) * (fa + t(1,i1))/2
46  endif
47  if(i2 .ne. n) then
48  fb = (t(1,i2+1) - t(1, i2))/ (xt(1,i2+1) - xt(1,i2)) *
49  * (bb -xt(1,i2)) + t(1,i2)
50  ans = ans+ (bb - xt(1,i2)) * (t(1,i2) + fb)/2
51  endif
52  do i = i1, i2-1
53  ans = ans + (xt(1,i+1) - xt(1, i)) * (t(1,i) + t(1,i+1))/2
54  enddo
ans
atmos%rho(atmos%nodes) **exp(-(z-atmos%z(atmos%nodes))/Hinf) elseif(z .lt. atmos%z(1)) then ans=atmos%rho(1) **exp((atmos%z(1) -z)/atmos%H(1)) else call kdwhereis(z, atmos%nodes, atmos%z, 1, i) a=atmos%a(i) if(a .ne. 0.d0) then ans=atmos%rho(i) **(1+a *(z-atmos%z(i))/atmos%H(i)) **(-1.0d0-1.d0/a) else ans=*atmos%rho(i) *exp(-(z-atmos%z(i))/atmos%H(i)) endif endif ! zsave=z ! endif cvh2den=ans end ! ---------------------------------- real *8 function cvh2temp(z) implicit none ! vettical height to temperatur(Kelvin) real *8 z ! input. vertical height in m ! output is temperature of the atmospher in Kelvin real *8 ans integer i if(z .gt. atmos%z(atmos%nodes)) then ans=atmos%T(atmos%nodes) elseif(z .lt. atmos%z(1)) then ans=atmos%T(1)+atmos%b(1) *(z - atmos%z(1)) else call kdwhereis(z, atmos%nodes, atmos%z, 1, i) ans=atmos%T(i)+atmos%b(i) *(z-atmos%z(i)) endif cvh2temp=ans end !--------------------------------------------- real *8 function cthick2h(t) implicit none real *8 t ! input. air thickness in kg/m^2 real *8 logt, ans integer i real *8 dod0, fd, a logt=log(t) if(t .ge. atmos%cumd(1)) then ans=atmos%z(1) - *(logt - atmos%logcumd(1)) *atmos%H(1) elseif(t .le. atmos%cumd(atmos%nodes)) then ans=atmos%z(atmos%nodes) - *Hinf *log(t/atmos%cumd(atmos%nodes)) else call kdwhereis(t, atmos%nodes, atmos%cumd, 1, i) ! i is such that X(i) > x >=x(i+1) ans
Definition: cstdatmos0.fNew2.h:82
i
nodes i
Definition: cstdatmos0.fNew2.h:93
nrl_atmos::a
real(4), save a
Definition: cNRLAtmos.f:20
t
nodes t
Definition: cstdatmos0.fNew2.h:84
nrl_atmos::b
real(4), save b
Definition: cNRLAtmos.f:21
n
integer n
Definition: Zcinippxc.h:1
Here is the caller graph for this function: